Bài 10 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và chính xác nhất cho Bài 10 trang 120 SGK Toán 11 tập 1 - Cánh Diều, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
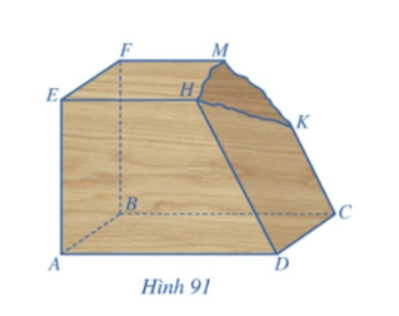
Một khối gỗ có các mặt đều là một phần của mặt phẳng với (ABCD) // (EFGH), CK // DH. Khối gỗ bị hỏng một góc (Hình 91). Bác thợ mộc muốn làm đẹp khối gỗ bằng cách cắt khối gỗ theo mặt phẳng (R) đi qua K và song song với mặt phẳng (ABCD).
Đề bài
Một khối gỗ có các mặt đều là một phần của mặt phẳng với (ABCD) // (EFGH), CK // DH. Khối gỗ bị hỏng một góc (Hình 91). Bác thợ mộc muốn làm đẹp khối gỗ bằng cách cắt khối gỗ theo mặt phẳng (R) đi qua K và song song với mặt phẳng (ABCD).
a) Hãy giúp bác thợ mộc xác định giao tuyến của mặt phẳng (R) với các mặt của khối gỗ để cắt được chính xác.
b) Gọi I, J lần lượt là giao điểm DH, BF với mặt phẳng (R). Biết BF = 60 cm, DH = 75 cm, CK = 40 cm. Tính FJ.
Phương pháp giải - Xem chi tiết
a, Tìm 2 điểm thuộc 2 mặt phẳng (P), (Q). Đường thẳng nối 2 điểm đó được gọi là giao tuyến của (P) và (Q).
b, Quan sát hình vẽ.
Lời giải chi tiết
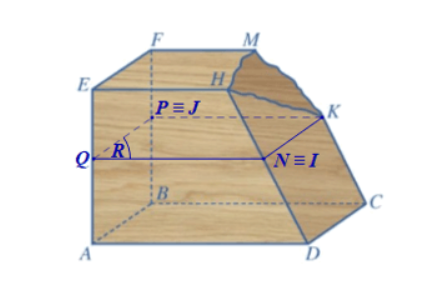
a) Trong mp(CDHK), qua K vẽ đường thẳng song song với CD, cắt DH tại N.
Trong mp(BCKF), qua K vẽ đường thẳng song song với BC, cắt BF tại P.
Ta có: NK // CD, mà CD ⊂ (ACBD) nên NK // (ABCD).
KP // BC, mà BC ⊂ (ACBD) nên KP // (ABCD).
NK, KP cắt nhau tại K trong mp(NPK).
Do đó (NPK) // (ABCD).
Khi đó mp(R) qua K và song song với (ABCD) chính là mp(NPK).
Trong mp(ADHE), qua N vẽ đường thẳng song song với AD, cắt AE tại Q.
Khi đó mp(R) là mp(NKPQ).
Vậy: (NKPQ) ∩ (ADHE) = QN;
(NKPQ) ∩ (CDHK) = NK;
(NKPQ) ∩ (BCKF) = KP;
(NKPQ) ∩ (ABFE) = PQ.
b)Ta có: DH cắt NK tại N, mà NK ⊂ (R) nên giao điểm của DH và (R) là điểm N.
Theo bài, I là giao điểm của DH và (R) nên điểm I và điểm N trùng nhau.
Tương tự ta cũng có điểm J trùng với điểm P.
Ta có: (ABCD) // (EFMH) và (R) // (ABCD) nên (EFMH) // (R) // (ABCD).
Lại có, hai cát tuyến FB, HD cắt ba mặt phẳng song song (EFMH), (R), (ABCD) lần lượt tại F, J, B và H, I, D nên theo định lí Thalès ta có: \(\frac{{FJ}}{{HI}} = \frac{{FB}}{{HD}}\) .
Mặt khác, trong mp(CDKH), tứ giác CDIK có CK // DI (do CK // DH) và IK // CD
Do đó CDIK là hình bình hành, suy ra DI = CK = 40 cm.
Khi đó HI = DH – DI = 75 – 40 = 35 (cm).
Vì vậy, từ \(\frac{{FJ}}{{HI}} = \frac{{FB}}{{HD}}\) ta có: \(\frac{{FJ}}{{35}} = \frac{{60}}{{75}}\) , suy ra \(FJ = \frac{{35.60}}{{75}} = 28\) (cm).
Vậy FJ = 28 cm.
Bài 10 trang 120 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh xác định mối quan hệ giữa các đường thẳng và mặt phẳng, tính góc giữa chúng, hoặc chứng minh tính song song, vuông góc.
Bài tập thường bao gồm các dạng câu hỏi sau:
Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức sau:
Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Giải:
Để củng cố kiến thức, học sinh có thể làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác.
Bài 10 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về đường thẳng và mặt phẳng trong không gian. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp học sinh tự tin hơn trong các kỳ thi.
Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các bạn học sinh sẽ hiểu rõ hơn về Bài 10 trang 120 SGK Toán 11 tập 1 - Cánh Diều và có thể tự giải các bài tập tương tự một cách dễ dàng.