Bài 7 trang 80 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc giải các bài toán liên quan đến phép biến hình. Bài tập này đòi hỏi học sinh nắm vững kiến thức về các phép biến hình cơ bản và cách áp dụng chúng vào giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 7 trang 80 SGK Toán 11 tập 1, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
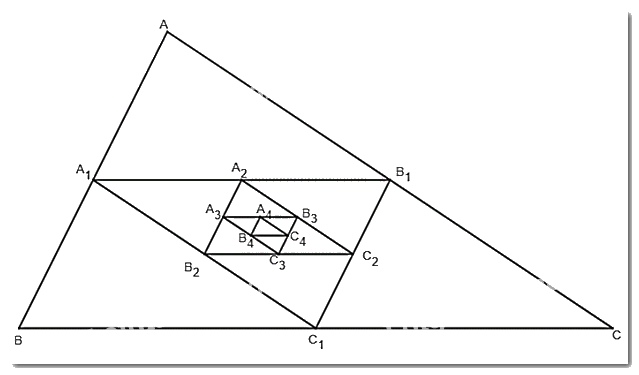
Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \)
Đề bài
Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \) Gọi \({p_1},{p_2}, \ldots ,{p_n}, \ldots \) và \({S_1},{S_2}, \ldots ,{S_n}, \ldots \) theo thứ tự là chu vi và diện tích của các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, \ldots ,{A_n}{B_n}{C_n}, \ldots \).
a) Tìm giới hạn của các dãy số \(\left( {{p_n}} \right)\) và \(\left( {{S_n}} \right)\).
b) Tìm các tổng \({p_1} + {p_2} + \ldots + {p_n} + \ldots \) và \({S_1} + {S_2} + \ldots + {S_n} + \ldots \).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\).
Chu vi tam giác bằng tổng ba cạnh.
Diện tích tam giác bằng một nửa chiều cao nhân cạnh đáy tương ứng.
Lời giải chi tiết
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
Bài 7 trong SGK Toán 11 tập 1 Cánh Diều là một bước quan trọng trong việc củng cố kiến thức về phép biến hình. Bài tập này không chỉ giúp học sinh hiểu rõ hơn về các loại phép biến hình như phép tịnh tiến, phép quay, phép đối xứng, mà còn rèn luyện kỹ năng áp dụng chúng vào giải quyết các bài toán thực tế.
Bài 7 tập trung vào việc xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép biến hình. Cụ thể, học sinh cần:
Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các công thức và tính chất của từng phép biến hình:
Ví dụ: Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 2) và vectơ v = (3; -1). Tìm tọa độ điểm M' là ảnh của M qua phép tịnh tiến theo vectơ v.
Giải: Áp dụng công thức phép tịnh tiến, ta có:
M'(x'; y') = M(1 + 3; 2 - 1) = M'(4; 1).
Để củng cố kiến thức, học sinh nên tự giải thêm các bài tập tương tự. Có thể tìm thấy các bài tập này trong sách bài tập Toán 11 tập 1 Cánh Diều hoặc trên các trang web học toán trực tuyến.
Việc nắm vững kiến thức về phép biến hình là nền tảng quan trọng cho việc học các chương trình Toán học nâng cao hơn, đặc biệt là hình học giải tích và hình học không gian. Ngoài ra, phép biến hình còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác như vật lý, kỹ thuật, và đồ họa máy tính.
Bài 7 trang 80 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về phép biến hình và ứng dụng của chúng. Bằng cách nắm vững kiến thức lý thuyết và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài toán liên quan đến phép biến hình một cách hiệu quả.