Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 112, 113 và 114 sách giáo khoa Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Hãy nêu lại công thức tính thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác.
Hãy nêu lại công thức tính thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác.
Phương pháp giải:
Nhớ lại công thức để nêu ra.
Lời giải chi tiết:
Thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
V = B.h với B là diện tích đáy, h là chiều cao khối lăng trụ.
Tính thể tích của khối lăng trụ \(ABC.A'B'C'\)' biết tất cả các cạnh bằng \(a\) và hình chiếu của \(A'\) trên mặt phẳng \(\left( {ABC} \right)\) là trung điểm của \(AB\).
Phương pháp giải:
Sử dụng công thức tính thể tích khối lăng trụ: \(V = Sh\).
Lời giải chi tiết:
Gọi \(H\) là trung điểm của \(AB\)\( \Rightarrow A'H \bot \left( {ABC} \right)\)
\(AH = \frac{1}{2}AB = \frac{a}{2}\)
\(\Delta AA'H\) vuông tại \(H\)\( \Rightarrow A'H = \sqrt {AA{'^2} - A{H^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.A'H = \frac{{3{a^3}}}{8}\end{array}\)
Cho khối tứ diện đều \(ABCD\) cạnh \(a\). Chứng minh rằng thể tích của khối tứ diện đó bằng \(\frac{{{a^3}\sqrt 2 }}{{12}}\).
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).
Lời giải chi tiết:

Gọi \(M\) là trung điểm của \(BC\), \(O\) là trọng tâm tam giác \(ABC\).
\( \Rightarrow SO \bot \left( {ABC} \right)\)
Tam giác \(ABC\) đều
\( \Rightarrow AM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
Tam giác \(SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SO = \frac{{{a^3}\sqrt 2 }}{{12}}\end{array}\)
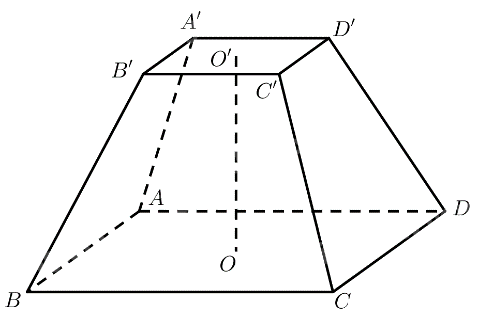
Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt dài 2 dm và 3 dm, chiều cao bằng 4 dm. Tính thể tích của thùng đựng rác.
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
Lời giải chi tiết:

Diện tích đáy lớn là: \(S = A{B^2} = {3^2} = 9\)
Diện tích đáy bé là: \(S' = {2^2} = 4\)
Thể tích hình chóp cụt là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.4\left( {9 + \sqrt {9.4} + 4} \right) = \frac{{76}}{3} \approx 25,3\left( {d{m^3}} \right)\)
Mục 3 trong SGK Toán 11 tập 2 - Cánh Diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào phân tích từng bài tập, cung cấp lời giải chi tiết và giải thích rõ ràng các bước thực hiện.
Bài tập này yêu cầu học sinh giải các phương trình lượng giác cơ bản, sử dụng các công thức biến đổi lượng giác và các phương pháp giải phương trình quen thuộc. Ví dụ, để giải phương trình sin(x) = a, ta cần xác định các nghiệm tổng quát và tìm các nghiệm thuộc khoảng cho trước.
Các bài tập nâng cao thường đòi hỏi học sinh phải vận dụng linh hoạt các công thức lượng giác, kết hợp với các kỹ năng biến đổi đại số và tư duy logic. Một số phương pháp giải thường được sử dụng bao gồm đặt ẩn phụ, sử dụng công thức cộng và trừ góc, và biến đổi phương trình về dạng cơ bản.
Bài tập ứng dụng giúp học sinh hiểu rõ hơn về vai trò của phương trình lượng giác trong việc mô tả và giải quyết các vấn đề thực tế. Ví dụ, ta có thể sử dụng phương trình lượng giác để tính góc nâng, góc hạ, hoặc chiều cao của một vật thể.
Để giải phương trình cos(2x) = 1/2, ta thực hiện các bước sau:
Vậy, phương trình cos(2x) = 1/2 có hai nghiệm thuộc khoảng (0, 2π) là x = π/6 và x = 7π/6.
Việc giải các bài tập trong mục 3 trang 112, 113, 114 SGK Toán 11 tập 2 - Cánh Diều đòi hỏi sự nắm vững kiến thức lý thuyết, kỹ năng giải toán và tư duy logic. Hy vọng rằng, với những hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập và đạt kết quả tốt nhất trong học tập.