Chào mừng bạn đến với bài giải Bài 14 trang 41 SGK Toán 11 tập 1 - Cánh diều trên giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ bạn trong quá trình chinh phục môn Toán.
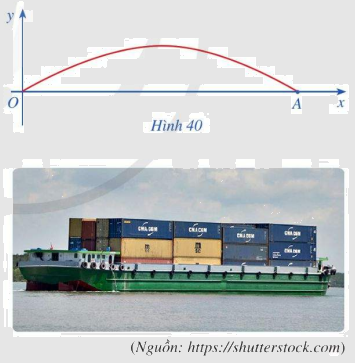
Một cây cầu có dạng cung OA của đồ thị hàm số (y = 4,8sin frac{x}{9}) và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như ở Hình 40.
Đề bài
Một cây cầu có dạng cung OA của đồ thị hàm số \(y = 4,8\sin \frac{x}{9}\) và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như ở Hình 40.
a) Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tìm chiều rộng đó (Làm tròn kết quả đến hàng phần mười)
b) Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 3,6m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hóa đó phải nhỏ hơn 13,1m.
c) Một sà lan khác cũng chở khối hàng hóa được xếp thành hình hộp chữ nhật với chiều rộng của khối hàng hóa đó là 9m sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều cao của khối hàng hóa đó phải nhỏ hơn 4,3m
Phương pháp giải - Xem chi tiết
Dựa vào hàm số lượng giác sin
Lời giải chi tiết
a) Hai vị trí \(O\) và \(A\) là hai vị trí chân cầu, tại hai vị trí này ta có: \(y = 0\)
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 0 \Leftrightarrow \sin \frac{x}{9} = 0 \Leftrightarrow \frac{x}{9} = k\pi (k \in \mathbb{Z}) \Leftrightarrow x = 9k\pi (k \in \mathbb{Z})\)
Quan sát đồ thị ta thấy, đồ thị hàm số \({\rm{y}} = 4,8 \cdot \sin \frac{x}{9}\) cắt trục hoành tại điểm 0 và \({\rm{A}}\) liên tiếp nhau với \(x \ge 0\).
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} = 0\);
Xét \({\rm{k}} = 1\), ta có \({{\rm{x}}_2} = 9\pi \).
Mà \({x_1} = 0\) nên đây là hoành độ của 0 , do đó \({x_2} = 9\pi \) là hoành độ của điểm \(A\).
Khi đó \(OA = 9\pi \approx 28,3\).
Vậy chiều rộng của con sông xấp xỉ 28,3 m.
b) Do sà lan có độ cao 3,6 m so với mực nước sông nên khi sà lan đi qua gầm cầu thì ứng với \({\rm{y}} = 3,6\).
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 3,6 \Leftrightarrow \sin \frac{x}{9} = \frac{3}{4} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\frac{{\rm{x}}}{9} \approx 0,848 + {\rm{k}}2\pi }\\{\frac{{\rm{x}}}{9} \approx \pi - 0,848 + {\rm{k}}2\pi }\end{array}} \right.\)
(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp \(SHIFT\)\sin 3 \div 4 = ta được kết quả gần đúng là 0,85) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{\rm{x}} \approx 7,632 + 18{\rm{k}}\pi }\\{{\rm{x}} \approx 9\pi - 7,632 + 18{\rm{k}}\pi }\end{array}({\rm{k}} \in \mathbb{Z})} \right.\)
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} \approx 7,632;{{\rm{x}}_2} \approx 20,642\).
Ta biểu diễn các giá trị \(x\) vừa tìm được trên hệ trục tọa độ vẽ đồ thị hàm số \(y = \) 4,8. \(\sin \frac{x}{9}\) như sau:
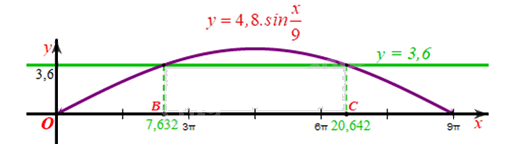
Khi đó để sà lan có thể đi qua được gầm cầu thì khối hàng hóa có độ cao 3,6 m phải có chiều rộng nhỏ hơn độ dài đoạn thẳng \({\rm{BC}}\) trên hình vẽ.
Mà \(BC \approx 20,642 - 7,632 = 13,01(m) < 13,1(m)\).
Vậy chiều rộng của khối hàng hoá đó phải nhỏ hơn 13,1 m.
c) Giả sử sà lan chở khối hàng được mô tả bởi hình chữ nhật MNPQ:
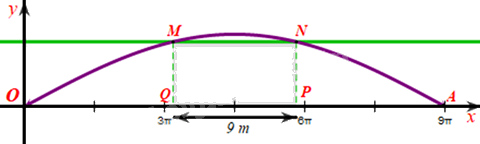
Khi đó \(QP = 9;OA = 28,3\) và \(OQ = PA\).
Mà \(OQ + QP + PA = OA \Rightarrow OQ + 9 + OQ \approx 28,3 \Rightarrow OQ \approx 9,65\)
Khi đó \({y_M} = 4,8 \cdot \sin \frac{{{x_M}}}{9} = 4,8 \cdot \sin \frac{{OQ}}{9} \approx 4,8 \cdot \sin \frac{{9,65}}{9} \approx 4,22(\;{\rm{m}}) < 4,3\) (m).
Vậy để sà lan có thể đi qua được gầm cầu thì chiều cao của khối hàng hoá đó phải nhỏ hơn 4,3 m.
Bài 14 trang 41 SGK Toán 11 tập 1 - Cánh diều thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 1: Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng các kiến thức về vectơ, phép toán vectơ, và các ứng dụng của vectơ để giải quyết các bài toán cụ thể.
Bài 14 bao gồm các dạng bài tập sau:
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi:
Đề bài: Cho A(1; 2), B(3; 4). Tìm tọa độ của vectơ AB.
Lời giải:
Vectơ AB có tọa độ là (3 - 1; 4 - 2) = (2; 2).
Đề bài: Cho vectơ a = (1; -2), b = (3; 1). Tìm tọa độ của vectơ a + b.
Lời giải:
Vectơ a + b có tọa độ là (1 + 3; -2 + 1) = (4; -1).
Đề bài: Cho vectơ a = (2; 3), k = -2. Tìm tọa độ của vectơ ka.
Lời giải:
Vectơ ka có tọa độ là (-2 * 2; -2 * 3) = (-4; -6).
Để giải tốt bài tập này, các bạn cần:
Ví dụ 1: Cho A(0; 0), B(1; 1), C(2; 0). Chứng minh rằng A, B, C không thẳng hàng.
Lời giải:
Ta có vectơ AB = (1; 1) và vectơ AC = (2; 0). Vì tỉ số giữa các tọa độ của hai vectơ này không bằng nhau (1/2 ≠ 1/0), nên A, B, C không thẳng hàng.
Bài 14 trang 41 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và các ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức. Chúc các bạn học tập tốt!