Bài 6 trang 100 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh diều, tập trung vào việc vận dụng kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này đòi hỏi học sinh phải nắm vững các khái niệm về vectơ, phép toán vectơ và ứng dụng của chúng trong không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 6 trang 100 SGK Toán 11 tập 1, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ. a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành. b) Chứng minh rằng (IK//BC) c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC)
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ.
a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành.
b) Chứng minh rằng \(IK//BC\)
c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC)
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Đường trung bình của tam giác:
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Dấu hiệu nhận biết hình bình hành:
Hình có một cặp cạnh đối song song và bằng nhau là hình bình hành.
Lời giải chi tiết
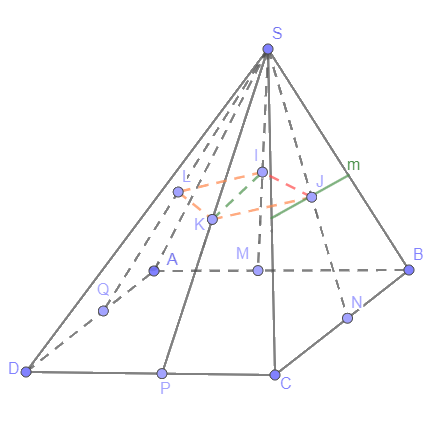
a) Tam giác ABC có M, N là trung điểm của AB, BC nên MN // AC (1)
Tam giác ACD có P, Q là trung điểm của CD, DA nên PQ // AC (2)
Tam giác SMN có I, J là trung điểm của SM, SN nên IJ // MN (3)
Tam giác SPQ có L, K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1), (2), (3), (4) suy ra IJ // LK
Suy ra I, J, K, L đồng phẳng
Ta có:\(\frac{{MN}}{{AC}} = \frac{{QP}}{{AC}} = \frac{1}{2}\)
\(\frac{{{\rm{IJ}}}}{{MN}} = \frac{{LK}}{{PQ}} = \frac{1}{2}\)
Suy ra IJ = LK mà IJ // LK
Suy ra IJKL là hình bình hành
b) Ta có M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
Tam giác SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1) và (2) suy ra: IK // BC
c) Ta có: J là giao điểm của hai mặt phẳng (IJKL) và (SBC)
mà IK // BC
Từ J kẻ Jm // BC
Suy ra Jm là giao tuyến của hai mặt phẳng (IJKL) và (SBC)
Bài 6 trang 100 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng trong hình học không gian. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 6 yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh một số đẳng thức vectơ hoặc giải quyết các bài toán liên quan đến vị trí tương đối của các điểm trong không gian.
Để giải bài tập này, học sinh cần:
Ví dụ, nếu bài tập yêu cầu chứng minh A, B, C thẳng hàng, ta có thể sử dụng điều kiện: AB = kAC, với k là một số thực.
Để giải các bài tập tương tự, học sinh có thể áp dụng các bước sau:
Giả sử bài tập yêu cầu chứng minh rằng bốn điểm A(1; 2; 3), B(2; 3; 4), C(3; 4; 5), D(4; 5; 6) cùng nằm trên một mặt phẳng.
Ta có thể giải bài tập này bằng cách tính các vectơ AB, AC và AD, sau đó tính tích hỗn hợp của ba vectơ này. Nếu tích hỗn hợp bằng 0, thì bốn điểm A, B, C, D cùng nằm trên một mặt phẳng.
Tích hỗn hợp được tính như sau: [AB, AC, AD] = (AB x AC) . AD
Sau khi tính toán, nếu kết quả bằng 0, ta kết luận bốn điểm cùng nằm trên một mặt phẳng.
Khi giải các bài tập về vectơ, học sinh cần chú ý đến các dấu và thứ tự của các vectơ. Việc nhầm lẫn về dấu hoặc thứ tự có thể dẫn đến kết quả sai.
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh có thể tự giải các bài tập sau:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ hiểu rõ hơn về Bài 6 trang 100 SGK Toán 11 tập 1 - Cánh diều và có thể tự tin giải quyết các bài tập tương tự.