Bài 7 trang 100 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của các cạnh BC, CD. Trên cạnh AC lấy điểm K. Gọi M là giao điểm của BK và AI, N là giao điểm của DK và AJ. Chứng minh rằng đường thẳng MN song song với đường thẳng BD.
Đề bài
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của các cạnh BC, CD. Trên cạnh AC lấy điểm K. Gọi M là giao điểm của BK và AI, N là giao điểm của DK và AJ. Chứng minh rằng đường thẳng MN song song với đường thẳng BD.
Phương pháp giải - Xem chi tiết
Áp dụng định lí Ta Lét đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết
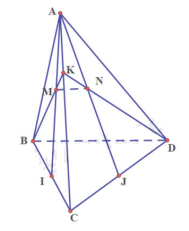
Giả sử K là trung điểm của AC
Suy ra M,N lần lượt là trọng tâm của tam giác ABC và tam giác ACD
Do đó, tam giác KBC có:\(\frac{{KM}}{{KB}} = \frac{{KN}}{{KD}} = \frac{1}{3}\)
Suy ra MN // BD
Chứng minh tương tự với trường hợp K bất kỳ
Bài 7 trang 100 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức liên quan.
Bài 7 yêu cầu học sinh giải các bài toán liên quan đến việc tính đạo hàm của hàm số, tìm cực trị của hàm số và khảo sát hàm số. Các bài toán này thường có dạng phức tạp, đòi hỏi học sinh phải có kỹ năng phân tích và giải quyết vấn đề tốt.
Để giải bài 7 trang 100 SGK Toán 11 tập 1 - Cánh diều, học sinh có thể áp dụng các phương pháp sau:
Cho hàm số y = x3 - 3x2 + 2. Hãy tìm đạo hàm của hàm số.
Giải:
Đạo hàm của hàm số y = x3 - 3x2 + 2 là:
y' = 3x2 - 6x
Tìm cực đại và cực tiểu của hàm số y = x4 - 4x2 + 3.
Giải:
Đạo hàm của hàm số y = x4 - 4x2 + 3 là:
y' = 4x3 - 8x
Giải phương trình y' = 0, ta được:
4x3 - 8x = 0
=> 4x(x2 - 2) = 0
=> x = 0 hoặc x = ±√2
Xét dấu của y', ta thấy:
Vậy hàm số đạt cực đại tại x = -√2 và x = √2, đạt cực tiểu tại x = 0.
Khi giải bài 7 trang 100 SGK Toán 11 tập 1 - Cánh diều, học sinh cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, như:
Bài 7 trang 100 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Hy vọng với lời giải chi tiết và phân tích trên, học sinh có thể tự tin giải bài tập và đạt kết quả tốt trong môn Toán.