Bài 5 trang 75 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Cánh Diều, tập trung vào việc giải các bài toán liên quan đến đạo hàm của hàm số. Bài tập này đòi hỏi học sinh nắm vững kiến thức về các quy tắc tính đạo hàm và ứng dụng chúng vào giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
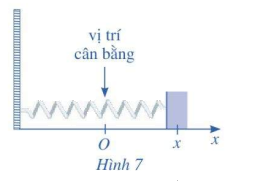
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát như Hình 7
Đề bài
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát như Hình 7 , có phương trình chuyển động \(x = 4\sin t\), trong đó t tính bằng giây và x tính bằng centimet.
a) Tìm vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm t (s)
b) Tìm vị trí, vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm \(t = \frac{{2\pi }}{3}(s)\)
Tại thời điểm đó, con lắc di chuyển theo hướng nào?
Phương pháp giải - Xem chi tiết
Dựa vào hàm số đạo hàm để tìm từng đại lượng sau đó thay số
Lời giải chi tiết
a) Vận tốc tức thời tại thời điểm t: \(v(t) = x' = 4\cos t\)
Gia tốc tức thời tại thời điểm t: \(a(t) = v'(t) = - 4\sin t\)
b) Tại thời điểm \(t = \frac{{2\pi }}{3}(s)\)
- Vận tốc tức thời là: \(v\left( {\frac{{2\pi }}{3}} \right) = 4\cos \frac{{2\pi }}{3} = - 2\)
- Gia tốc tức thời là: \(a\left( {\frac{{2\pi }}{3}} \right) = - 4\sin \frac{{2\pi }}{3} = - 2\sqrt 3 \)
- Tại thời điểm đó, con lắc đang di chuyển theo hướng ngược chiều dương
Bài 5 trang 75 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 5 yêu cầu học sinh tính đạo hàm của các hàm số sau:
a) y = x3 - 3x2 + 2x - 5
Áp dụng quy tắc đạo hàm của tổng và hiệu, ta có:
y' = 3x2 - 6x + 2
b) y = (x2 + 1)(x - 2)
Áp dụng quy tắc đạo hàm của tích, ta có:
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
c) y = (x2 + 3x + 1) / (x + 1)
Áp dụng quy tắc đạo hàm của thương, ta có:
y' = [(2x + 3)(x + 1) - (x2 + 3x + 1)(1)] / (x + 1)2 = (2x2 + 5x + 3 - x2 - 3x - 1) / (x + 1)2 = (x2 + 2x + 2) / (x + 1)2
d) y = sin(2x + 1)
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(2x + 1) * 2 = 2cos(2x + 1)
e) y = cos(x2)
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = -sin(x2) * 2x = -2xsin(x2)
Để giải các bài tập tương tự, học sinh cần nắm vững các quy tắc đạo hàm cơ bản sau:
Ngoài ra, học sinh cần nhớ các đạo hàm cơ bản của các hàm số lượng giác như sin(x), cos(x), tan(x), cot(x).
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Việc nắm vững kiến thức về đạo hàm là rất quan trọng để học tốt môn Toán 11 và chuẩn bị cho các kỳ thi quan trọng.
Để củng cố kiến thức, học sinh có thể tự giải các bài tập sau:
Hy vọng với lời giải chi tiết và hướng dẫn trên, học sinh có thể hiểu rõ và tự tin giải Bài 5 trang 75 SGK Toán 11 tập 2 - Cánh Diều.