Bài viết này cung cấp lý thuyết đầy đủ và chi tiết về các khái niệm quan trọng trong chương trình Toán 11 Cánh diều, bao gồm biến cố hợp, biến cố giao, biến cố độc lập và các quy tắc tính xác suất. Chúng tôi sẽ giúp bạn hiểu rõ bản chất của từng khái niệm và cách áp dụng chúng vào giải các bài toán thực tế.
Với phương pháp trình bày dễ hiểu, kèm theo các ví dụ minh họa cụ thể, bạn sẽ dễ dàng nắm bắt kiến thức và tự tin hơn trong quá trình học tập và làm bài tập.
Xét phép tử T có không gian mẫu là tập hợp (Omega ) gồm hữu hạn phần tử; các kết quả của phép thử là đồng khả năng, các biến cố đều liên quan đến phép thử đó.
Xét phép tử T có không gian mẫu là tập hợp \(\Omega \) gồm hữu hạn phần tử; các kết quả của phép thử là đồng khả năng, các biến cố đều liên quan đến phép thử đó.
a) Biến cố hợp
Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu \(\Omega \). Đặt \(C = A \cup B\), ta có C là một biến cố và được gọi là biến cố hợp của hai biến cố A và B, kí hiệu là \(A \cup B\).
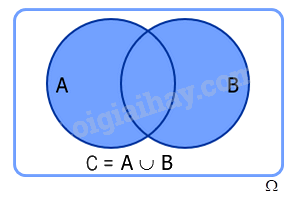
b) Biến cố giao
Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu \(\Omega \). Đặt \(D = A \cap B\), ta có D là một biến cố và được gọi là biến cố giao của hai biến cố A và B, kí hiệu là \(A \cap B\) hay AB.
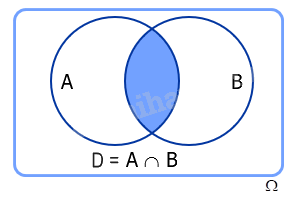
c) Biến cố xung khắc
Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu \(\Omega \). Nếu \(A \cap B = \emptyset \) thì A và B gọi là hai biến cố xung khắc.
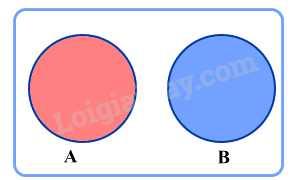
Cho hai biến cố A và B. Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia.
Chú ý: Nếu A, B là hai biến cố độc lập thì mỗi cặp biến cố sau cũng độc lập: A và \(\overline B \); \(\overline A \) và B; \(\overline A \) và \(\overline B \).
a) Công thức cộng xác suất
Cho hai biến cố A và B. Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)\).
Hệ quả: Nếu hai biến cố A và B là xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
b) Công thức nhân xác suất
Cho hai biến cố A và B. Nếu hai biến cố A và B là độc lập thì \(P\left( {A \cap B} \right) = P\left( A \right).P\left( B \right)\).
Bài 1. Gieo hai con xúc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con xúc xắc bằng 7 là:
A. \(\dfrac{2}{9}\).
B. \(\dfrac{1}{6}\).
C. \(\dfrac{7}{{36}}\).
D. \(\dfrac{5}{{36}}\).
Lời giải: Ta có: \(n(\Omega ) = 6.6 = 36\).
Gọi \(A\):”tổng số chấm trên mặt xuất hiện của hai con súc sắc bằng 7”.
\(A = {\rm{\{ (1;6);(2;5);(3;4);(4;3);(5;2);(6;1)\} }}\).
Do đó \(n(A) = 6\).
Vậy \(P(A) = \dfrac{6}{{36}} = \dfrac{1}{6}\).
Chọn đáp án B
Bài 2. Gieo đồng xu hai lần liên tiếp. Biến cố \(A\) là biến cố “Mặt ngửa xuất hiện đúng 1 lần”. Số phần tử của \({\Omega _A}\) là:
A. \(2\)
B. \(1\)
C. \(3\)
D. \(4\)
Lời giải:
Ta có: \({\Omega _A} = \left\{ {NS,SN} \right\}\).
Chọn đáp án A.
Bài 3. Cho phép thử có không gian mẫu \(\Omega = \left\{ {1;2;3;4;5;6} \right\}\). Cặp biến cố không đối nhau là:
A. \(A = \left\{ 1 \right\}\) và \(B = \left\{ {2;3;4;5;6} \right\}\)
B. \(C = \left\{ {1;2;5} \right\}\) và \(D = \left\{ {3;4;6} \right\}\)
C. $E = \left\{ {1;4;6} \right\}$ và \(F = \left\{ {2;3} \right\}\)
D. \(G = \Omega \) và \(H = \emptyset \)
Lời giải:
Trong các đáp án đã cho ta thấy chỉ có đáp án C là không thỏa mãn điều kiện của biến cố đối.
Chọn đáp án C.
Bài 4. Có $8$ quả cân lần lượt là $1kg, 2kg, 3kg, 4kg, 5kg, 6kg, 7kg, 8kg$. Chọn ngẫu nhiên $3$ quả cân trong $8$ quả cân đó. Tính xác suất để trọng lượng $3$ quả cân được chọn không vượt quá $9kg$.
A. \(\dfrac{1}{{15}}\)
B. \(\dfrac{1}{7}\)
C. \(\dfrac{1}{{28}}\)
D. \(\dfrac{1}{8}\)
Lời giải: Chọn ngẫu nhiên $3$ quả cân trong $8$ quả cân ta có \(\left| \Omega \right| = C_8^3 = 56\)
Gọi $A$ là biến cố chọn được $3$ quả cân và tổng trọng lượng $3$ quả cân không vượt quá $9 kg$.
Vì
\(\begin{array}{l}1 + 2 + 3 = 6 < 9\\1 + 2 + 4 = 7 < 9\\1 + 2 + 5 = 8 < 9\\1 + 2 + 6 = 9\\1 + 3 + 4 = 8 < 9\\1 + 3 + 5 = 9\\2 + 3 + 4 = 9\end{array}\)
Nên \(\left| A \right| = 7\)
Vậy \(P(A) = \dfrac{{\left| A \right|}}{{\left| \Omega \right|}} = \dfrac{7}{{56}} = \dfrac{1}{8}\)
Chọn đáp án D.
Bài 5. Một chiếc tàu khoan thăm dò dầu khí trên thềm lục địa có xác suất khoan trúng túi dầu là $0,4$. Xác suất để trong $5$ lần khoan độc lập, chiếc tàu đó khoan trúng túi dầu ít nhất một lần.
A. \(0,07776\)
B. \(0,84222\)
C. \(0,15778\)
D. \(0,92224\)
Lời giải:
Gọi A là biến cố “chiếc tàu khoan trúng túi dầu”. Ta có \(P\left( A \right) = 0,4\)
Suy ra \(\bar A\) là biến cố “chiếc tàu khoan không trúng túi dầu”. Ta có \(P(\bar A) = 0,6\)
Xét phép thử “tàu khoan 5 lần độc lập” với biến cố
B:“chiếc tàu không khoan trúng túi dầu lần nào”, ta có \(P(B) = 0,{6^5} = 0,07776\)
Khi đó ta có \(\overline B\) “chiếc tàu khoan trúng túi dầu ít nhất một lần”. Ta có:
\(P\left( {\overline B} \right) = 1 - P(B) \) \(= 1 - 0,07776 = 0,92224\)
Chọn đáp án D.
Bài 6. Một trạm điều động xe có 15 xe ô tô trong đó có 10 xe tốt và 5 xe không tốt. Trạm xe điều động ngẫu nhiên 4 xe ô tô đi chở khách, xác suất để trong 4 xe ô tô có ít nhất 1 xe tốt là:
A. \(\frac{{273}}{{1365}}\)
B. \(\frac{{272}}{{273}}\)
C. \(\frac{1}{{273}}\)
D. \(\frac{{1364}}{{1365}}\)
Lời giải:
Số phần tử của không gian mẫu là \(n\left( \Omega \right) = C_{15}^4 = 1365\).
Gọi A là biến cố: “trong 4 xe ô tô có ít nhất 1 xe tốt” \( \Rightarrow \) Biến cố đối \(\overline A \) “trong 4 xe ô tô có không có xe tốt nào”.
\( \Rightarrow n\left( {\overline A } \right) = C_5^4 = 5\).
Vậy xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{5}{{1365}} = \frac{{272}}{{273}}\).
Chọn đáp án B.
Bài 7. Giả sử $A$ và $B$ là hai biến cố cùng liên quan đến phép thử $T$. Khẳng định nào trong các khẳng định sau là đúng?
1) Nếu $A $ và $B$ là hai biến cố độc lập thì \(P(A \cup B) = P(A) + P(B)\) .
2) Nếu $A$ và $B$ là hai biến cố xung khắc thì \(P(A \cup B) = P(A) + P(B)\) .
3) \(P(AB) = P(A).P(B)\).
A. Chỉ 1 đúng
B. Chỉ 2 đúng
C. Chỉ 3 đúng
D. Cả ba đều sai.
Lời giải:
Dựa vào lý thuyết biến cố đối và biến cố độc lập ta có:
- Nếu $A$ và $B$ là hai biến cố độc lập thì \(P(AB) = P(A).P(B)\) .
- Nếu $A$ và $B$ là hai biến cố xung khắc thì \(P(A \cup B) = P(A) + P(B)\).
Vậy chỉ có $2$ đúng.
Chọn đáp án B.
Bài 8. Xác suất bắn trúng đích của một người bắn súng là $0,6$. Xác suất để trong ba lần bắn độc lập người đó bắn trúng đích đúng một lần.
A. \(0,4\)
B. \(0,6\)
C. \(0,096\)
D. \(0,288\)
Lời giải: Gọi A là biến cố “người bắn súng bắn trúng đích”. Ta có \(P\left( A \right) = 0,6\) Suy ra \(\overline A\) là biến cố “người bắn súng không bắn trúng đích”. Ta có \(P(\overline A) = 0,4\) Xét phép thử “bắn ba lần độc lập” với biến cố “người đó bắn trúng đích đúng một lần”, ta có các biến cố xung khắc sau: • \(B\): “Bắn trúng đích lần đầu và trượt ở hai lần bắn sau”. Ta có \(P(B) = 0,6.0,4.0,4 = 0,096\) • C: “Bắn trúng đích ở lần bắn thứ hai và trượt ở lần đầu và lần thứ ba”. Ta có \(P(C) = 0,4.0,6.0,4 = 0,096\) • D: “Bắn trúng đích ở lần bắn thứ ba và trượt ở hai lần đầu”. Ta có: \(P(D) = 0,4.0,4.0,6 = 0,096\) Xác suất để người đó bắn trúng đích đúng một lần là: \(P = P(A) + P(B) + P(C) = 0,096 + 0,096 + 0,096 = 0,288\)
Chọn đáp án D.
Bài 9. Hai cầu thủ bóng đá sút phạt đền, mỗi người được sút một quả với xác suất bàn tương ứng là $0,8$ và $0,7$. Tính xác suất để chỉ có $1$ cầu thủ làm bàn.
A. \(0,14\)
B. \(0,38\)
C. \(0,24\)
D. \(0,62\)
Lời giải: Gọi $A$ là biến cố cầu thủ thứ nhất ghi được bàn thắng.
Ta có \(P\left( A \right) = 0,8\) và \(P(\overline A ) = 0,2\)
Gọi $B$ là biến cố cầu thủ thứ nhất ghi được bàn thắng.
Ta có \(P\left( B \right) = 0,7\) và \(P(\overline B) = 0,3\)
Ta xét hai biến cố xung khắc sau:
\(A\overline B\) “Chỉ có cầu thủ thứ nhất làm bàn”.
Ta có:
\(P\left( {A\overline B} \right) = P\left( A \right).P\left( {\overline B} \right) \) \(= 0,8.0,3 = 0,24\)
\(B\bar A\) “ Chỉ có cầu thủ thứ hai làm bàn” .
Ta có:
$P\left( {B\overline A} \right) = P\left( B \right).P\left( {\overline A} \right) $ $= 0,7.0,2 = 0,14$
Gọi $C$ là biến cố chỉ có $1$ cầu thủ làm bàn.
Ta có \(P(C) = 0,24 + 0,14 = 0,38\)
Chọn đáp án B.
Chương trình Toán 11 Cánh diều, đặc biệt là phần xác suất, đòi hỏi học sinh phải nắm vững các khái niệm cơ bản và các quy tắc tính toán. Bài viết này sẽ đi sâu vào các nội dung chính sau:
Biến cố là một sự kiện mà chúng ta quan tâm khi thực hiện một phép thử. Ví dụ, khi tung một đồng xu, biến cố có thể là “mặt ngửa xuất hiện” hoặc “mặt sấp xuất hiện”.
Biến cố hợp của hai biến cố A và B (ký hiệu A ∪ B) là biến cố xảy ra khi ít nhất một trong hai biến cố A hoặc B xảy ra. Nói cách khác, A ∪ B xảy ra nếu A xảy ra, B xảy ra, hoặc cả A và B đều xảy ra.
Công thức tính xác suất của biến cố hợp:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Biến cố giao của hai biến cố A và B (ký hiệu A ∩ B) là biến cố xảy ra khi cả hai biến cố A và B đều xảy ra. Nói cách khác, A ∩ B chỉ xảy ra khi cả A và B đồng thời xảy ra.
Công thức tính xác suất của biến cố giao:
Nếu A và B độc lập: P(A ∩ B) = P(A) * P(B)
Nếu A và B không độc lập: P(A ∩ B) = P(A) * P(B|A) = P(B) * P(A|B)
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra của biến cố A không ảnh hưởng đến xác suất xảy ra của biến cố B, và ngược lại. Nói cách khác, P(A|B) = P(A) và P(B|A) = P(B).
Ví dụ: Tung đồng xu hai lần. Biến cố “lần tung thứ nhất ra mặt ngửa” và biến cố “lần tung thứ hai ra mặt sấp” là hai biến cố độc lập.
Ví dụ 1: Một hộp chứa 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 2 quả bóng. Tính xác suất để lấy được 2 quả bóng đỏ.
Giải:
Ví dụ 2: Tung hai con xúc xắc. Tính xác suất để tổng số chấm trên hai con xúc xắc bằng 7.
Giải:
Các trường hợp có tổng bằng 7: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1). Có tổng cộng 6 trường hợp.
Tổng số trường hợp khi tung hai con xúc xắc: 6 * 6 = 36
Xác suất để tổng số chấm bằng 7: P = 6/36 = 1/6
Để củng cố kiến thức, bạn có thể thực hành các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết biến cố hợp, biến cố giao, biến cố độc lập và các quy tắc tính xác suất trong chương trình Toán 11 Cánh diều. Chúc bạn học tập tốt!