Bài 5 trang 115 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12
Đề bài
Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3 g/cm.
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính thể tích khối lăng trụ: \(V = Sh\).
‒ Sử dụng công thức tính khối lượng: \(m = D.V\).
Lời giải chi tiết
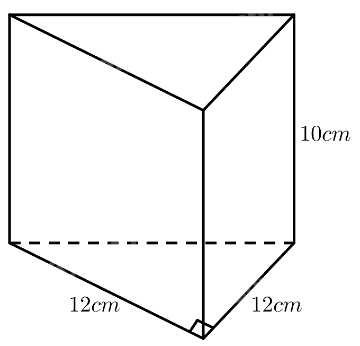
Diện tích đáy của miếng pho mát là: \(S = \frac{1}{2}.12.12 = 72\left( {c{m^2}} \right)\).
Thể tích của miếng pho mát là: \(V = Sh = 72.10 = 720\left( {c{m^3}} \right)\).
Khối lượng của miếng pho mát là: \(m = D.V = 3.720 = 2160\left( g \right)\).
Bài 5 trang 115 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
(Đề bài Bài 5 trang 115 SGK Toán 11 tập 2 - Cánh Diều được trình bày đầy đủ tại đây)
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
Ví dụ minh họa:
(Giải chi tiết một ví dụ cụ thể liên quan đến Bài 5 trang 115, bao gồm các bước tính toán và giải thích rõ ràng)
Để làm tốt các bài tập tương tự, bạn cần:
Đạo hàm là một khái niệm quan trọng trong giải tích, có nhiều ứng dụng trong các lĩnh vực khác nhau như vật lý, kinh tế, kỹ thuật,... Việc hiểu rõ về đạo hàm sẽ giúp bạn giải quyết các bài toán phức tạp hơn và có cái nhìn sâu sắc hơn về thế giới xung quanh.
Để củng cố kiến thức, bạn có thể làm thêm các bài tập sau:
Bài 5 trang 115 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập này, các bạn học sinh sẽ hiểu rõ hơn về đạo hàm và tự tin làm bài tập.
Lưu ý:
Hãy luôn kiểm tra lại kết quả của mình trước khi nộp bài. Nếu có bất kỳ thắc mắc nào, hãy hỏi giáo viên hoặc bạn bè để được giúp đỡ.
| Công thức đạo hàm | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x2)' = 2x |
| (sin x)' = cos x | (sin x)' = cos x |
| (cos x)' = -sin x | (cos x)' = -sin x |