Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 70, 71 SGK Toán 11 tập 1 - Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập trong mục 3 tập trung vào các kiến thức quan trọng của chương trình Toán 11, đòi hỏi các em phải có sự hiểu biết sâu sắc về lý thuyết và kỹ năng vận dụng linh hoạt.
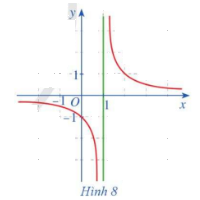
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\,\,\left( {x \ne 1} \right)\) có đồ thị như ở Hình 8. Quan sát đồ thị đó và cho biết: a) Khi biến x dần tới 1 về bên phải thì \(f\left( x \right)\) dần tới đâu. b) Khi biến x dần tới 1 về bên trái thì \(f\left( x \right)\) dần tới đâu
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\,\,\left( {x \ne 1} \right)\) có đồ thị như ở Hình 8. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới 1 về bên phải thì \(f\left( x \right)\) dần tới đâu.
b) Khi biến x dần tới 1 về bên trái thì \(f\left( x \right)\) dần tới đâu.
Phương pháp giải:
Quan sát đồ thị hình 8 để trả lời câu hỏi.
Lời giải chi tiết:
a) Khi biến x dần tới 1 về bên phải thì \(f\left( x \right)\) dần dương vô cực.
b) Khi biến x dần tới 1 về bên trái thì \(f\left( x \right)\) dần âm vô cực.
Tính: \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{1}{{x + 2}}.\)
Phương pháp giải:
Sử dụng giới hạn cơ bản sau: \(\mathop {\lim }\limits_{x \to {a^ - }} \frac{1}{{x - a}} = - \infty \)
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{1}{{x + 2}} = - \infty \)
Mục 3 trong SGK Toán 11 tập 1 - Cánh Diều thường xoay quanh các chủ đề về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức nền tảng về vectơ là vô cùng quan trọng để giải quyết các bài tập trong mục này một cách hiệu quả.
Trước khi đi vào giải bài tập cụ thể, chúng ta cần ôn lại một số kiến thức cơ bản về vectơ:
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong mục 3 trang 70, 71 SGK Toán 11 tập 1 - Cánh Diều:
Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b và a - b.
Lời giải:
Cho hai vectơ a = (2; -1) và b = (1; 3). Tính tích vô hướng của a và b.
Lời giải:
a.b = (2 * 1) + (-1 * 3) = 2 - 3 = -1
Để giải các bài tập về vectơ một cách nhanh chóng và hiệu quả, các em có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, các em nên luyện tập thêm với các bài tập khác trong SGK và các tài liệu tham khảo. Ngoài ra, các em có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kinh nghiệm và học hỏi lẫn nhau.
Vectơ có rất nhiều ứng dụng trong hình học, chẳng hạn như:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải các bài tập mục 3 trang 70, 71 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt!