Bài 6 trang 115 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc ôn tập chương 4: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số lượng giác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 6 trang 115 SGK Toán 11 tập 2 - Cánh Diều, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một loại đèn đá muối có dạng khối chóp tứ giác đều (Hình 97)
Đề bài
Một loại đèn đá muối có dạng khối chóp tứ giác đều (Hình 97). Tính theo \(a\) thể tích của đèn đá muối đó, giả sử các cạnh đáy và các cạnh bên đều bằng \(a\).

Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).
Lời giải chi tiết
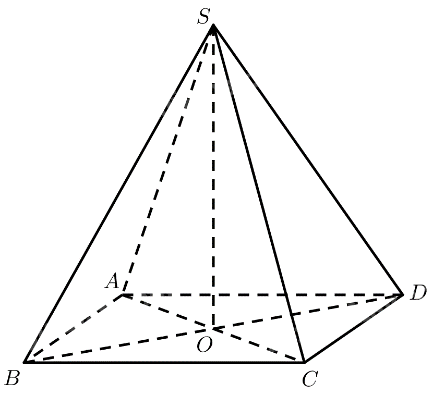
Mô hình hoá đèn đá muối bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\).
Gọi \(O\) là tâm của đáy.
\(\Delta SAC\) cân tại \(S\) \( \Rightarrow SO \bot AC\)
\(\Delta SBD\) cân tại \(S\) \( \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\\{V_{S.ABC{\rm{D}}}} = \frac{1}{3}.{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\end{array}\)
Bài 6 trang 115 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số lượng giác và ứng dụng của chúng. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 6 yêu cầu học sinh giải các bài toán liên quan đến việc xác định tập xác định của hàm số lượng giác, tìm giá trị của hàm số tại một điểm, và giải các phương trình lượng giác cơ bản. Cụ thể, bài tập có thể bao gồm các dạng sau:
Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức sau:
Ví dụ 1: Xác định tập xác định của hàm số y = tan(x)
Hàm số y = tan(x) = sin(x) / cos(x). Tập xác định của hàm số là tập hợp tất cả các giá trị của x sao cho cos(x) ≠ 0. Điều này có nghĩa là x ≠ π/2 + kπ, với k là số nguyên.
Ví dụ 2: Tính giá trị của sin(π/3) + cos(π/6)
Ta có sin(π/3) = √3/2 và cos(π/6) = √3/2. Do đó, sin(π/3) + cos(π/6) = √3/2 + √3/2 = √3.
Ví dụ 3: Giải phương trình sin(x) = 1/2
Phương trình sin(x) = 1/2 có hai nghiệm trong khoảng [0, 2π): x = π/6 và x = 5π/6. Nghiệm tổng quát của phương trình là x = π/6 + k2π và x = 5π/6 + k2π, với k là số nguyên.
Để giải các bài tập tương tự, học sinh nên:
Ngoài việc giải các bài tập trong SGK, học sinh nên tìm hiểu thêm về các ứng dụng của hàm số lượng giác trong thực tế, chẳng hạn như trong vật lý, kỹ thuật, và khoa học máy tính. Việc này sẽ giúp các em hiểu sâu hơn về tầm quan trọng của hàm số lượng giác và ứng dụng của chúng trong cuộc sống.
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh nên luyện tập thêm các bài tập tương tự trong các sách bài tập, đề thi thử, và các trang web học toán online. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn khi làm bài kiểm tra và thi cử.
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập Bài 6 trang 115 SGK Toán 11 tập 2 - Cánh Diều, các em học sinh sẽ nắm vững kiến thức và tự tin hơn trong quá trình học tập.