Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 96, 97 SGK Toán 11 tập 2 chương trình Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, tiết kiệm thời gian và đạt kết quả cao trong môn Toán.
Nền nhà, cánh cửa và mép cánh cửa ở Hình 48 gợi nên hình ảnh mặt mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\)
Nền nhà, cánh cửa và mép cánh cửa ở Hình 48 gợi nên hình ảnh mặt mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) và đường thẳng \(a\) nằm trên mặt phẳng \(\left( P \right)\). Quan sát Hình 48 và cho biết:
a) Vị trí tương đối của đường thẳng \(a\) và mặt phẳng \(\left( Q \right)\);
b) Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có vuông góc với nhau không.
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Đường thẳng \(a\) vuông góc với mặt phẳng \(\left( Q \right)\).
b) Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) vuông góc với nhau không.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(SA \bot \left( {ABCD} \right)\). Chứng minh rằng \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Phương pháp giải:
Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
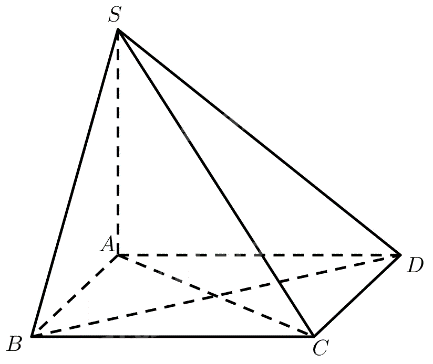
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot B{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\\B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow \left( {SAC} \right) \bot \left( {SB{\rm{D}}} \right)\)
Mục 2 của SGK Toán 11 tập 2 Cánh Diều tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để chứng minh mối quan hệ giữa đường thẳng và mặt phẳng, xác định góc giữa chúng, và giải các bài toán thực tế liên quan.
Bài tập này thường yêu cầu học sinh chứng minh hai đường thẳng song song, hai đường thẳng cùng song song với một mặt phẳng, hoặc một đường thẳng song song với một mặt phẳng. Để giải quyết các bài tập này, học sinh cần nắm vững các định lý về quan hệ song song trong không gian, đặc biệt là định lý về hai đường thẳng song song khi chúng song song với cùng một mặt phẳng.
Bài tập này thường yêu cầu học sinh chứng minh hai đường thẳng vuông góc, một đường thẳng vuông góc với một mặt phẳng, hoặc tính góc giữa hai đường thẳng, giữa một đường thẳng và một mặt phẳng. Để giải quyết các bài tập này, học sinh cần nắm vững các định lý về quan hệ vuông góc trong không gian, đặc biệt là định lý về đường thẳng vuông góc với mặt phẳng.
Ví dụ, để chứng minh một đường thẳng vuông góc với một mặt phẳng, ta cần chứng minh đường thẳng đó vuông góc với hai đường thẳng bất kỳ nằm trong mặt phẳng đó.
Bài tập này yêu cầu học sinh tính góc giữa hai đường thẳng hoặc giữa một đường thẳng và một mặt phẳng. Để giải quyết các bài tập này, học sinh cần sử dụng các công thức tính góc và nắm vững các khái niệm về hình chiếu của một đường thẳng lên một mặt phẳng.
Công thức tính góc giữa hai đường thẳng: cos(θ) = |(a.b)| / (||a|| * ||b||), trong đó a và b là vectơ chỉ phương của hai đường thẳng.
Công thức tính góc giữa đường thẳng và mặt phẳng: sin(θ) = |(a.n)| / (||a|| * ||n||), trong đó a là vectơ chỉ phương của đường thẳng và n là vectơ pháp tuyến của mặt phẳng.
Kiến thức về đường thẳng và mặt phẳng trong không gian có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, kỹ thuật, và đồ họa máy tính. Ví dụ, trong kiến trúc, việc xác định góc giữa các mặt phẳng, khoảng cách giữa các đường thẳng là rất quan trọng để thiết kế các công trình đảm bảo tính thẩm mỹ và an toàn.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin giải quyết các bài tập mục 2 trang 96, 97 SGK Toán 11 tập 2 Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao!