Chào mừng bạn đến với bài học về lý thuyết Đường thẳng và mặt phẳng song song, một phần quan trọng trong chương trình Hình học không gian lớp 11 theo SGK Toán 11 Cánh Diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để giải quyết các bài toán liên quan đến chủ đề này.
Chúng ta sẽ cùng nhau khám phá các định nghĩa, tính chất, và điều kiện để hai đường thẳng hoặc hai mặt phẳng song song. Đồng thời, bài học cũng sẽ hướng dẫn bạn cách áp dụng các kiến thức này vào việc giải các bài tập thực tế.
I. Đường thẳng song song với mặt phẳng
I. Đường thẳng song song với mặt phẳng
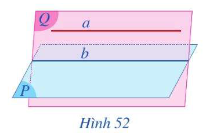
Đường thẳng được gọi là song song với mặt phẳng nếu chúng không có điểm chung.
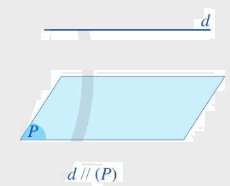
*Nhận xét:
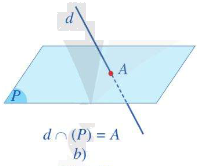
- Nếu d và \(\left( P \right)\) có một điểm chung duy nhất thì ta nói d và \(\left( P \right)\) cắt nhau tại A. Kí hiệu \(d \cap \left( P \right) = A\)hay \(d \cap \left( P \right) = \left\{ A \right\}\).
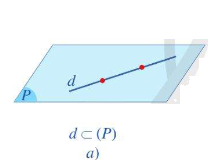
- Nếu d và \(\left( P \right)\) có nhiều hơn 1 điểm chung thì ta nói d nằm trong \(\left( P \right)\) hay \(\left( P \right)\) chứa d. Kí hiệu \(d \subset \left( P \right)\)hay \(\left( P \right) \supset d\).
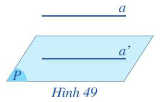
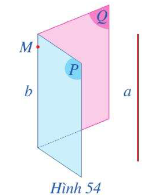
II. Điều kiện và tính chất
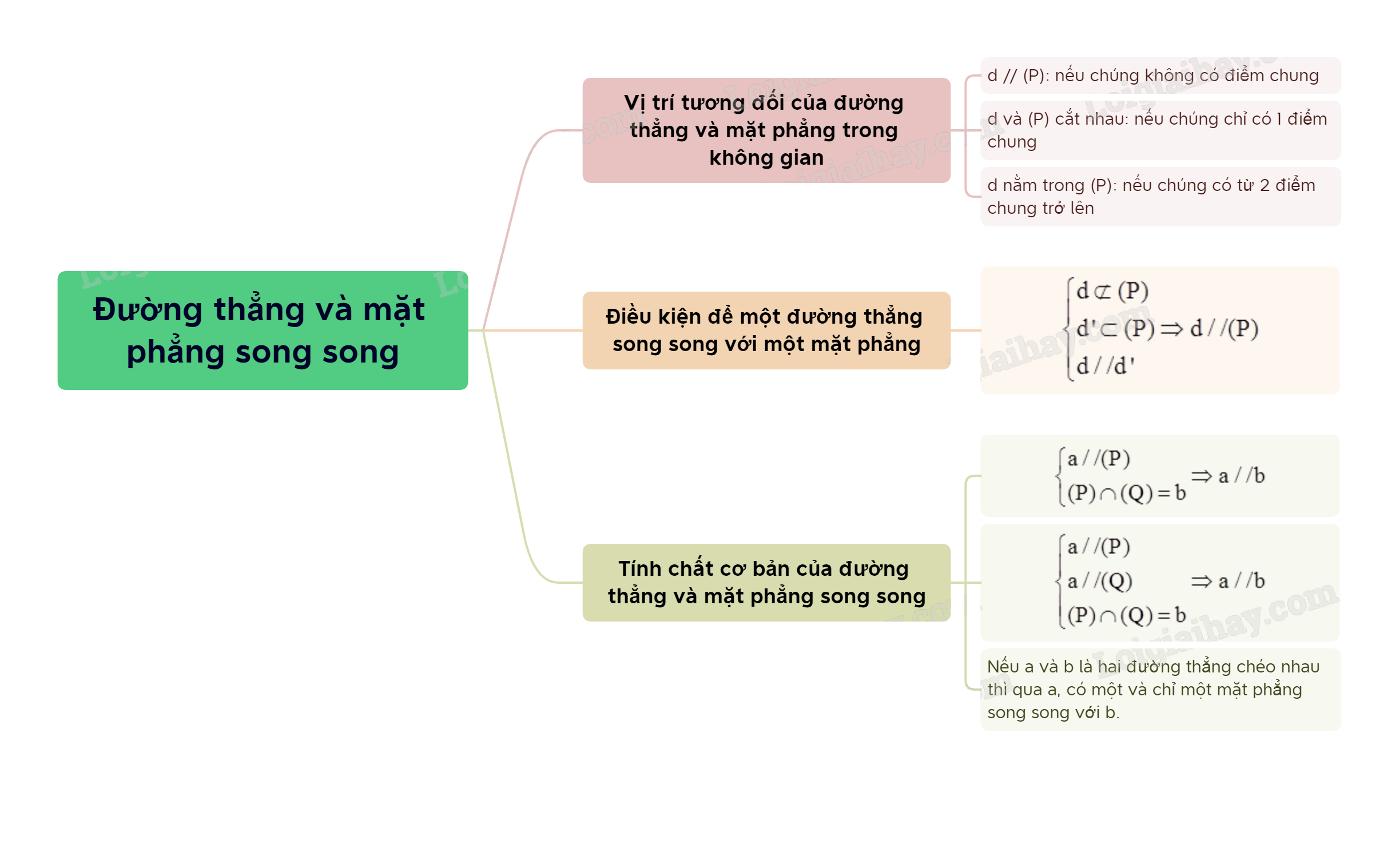
Chương trình Hình học không gian trong Toán 11 đóng vai trò quan trọng trong việc phát triển tư duy không gian và khả năng giải quyết vấn đề. Một trong những chủ đề cốt lõi của chương này là lý thuyết về đường thẳng và mặt phẳng song song. Bài viết này sẽ trình bày chi tiết lý thuyết này dựa trên nội dung SGK Toán 11 Cánh Diều, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập liên quan.
1. Đường thẳng song song:
2. Mặt phẳng song song:
3. Đường thẳng song song với mặt phẳng:
1. Nếu a // b và (P) chứa a thì (P) // b hoặc (P) và b không có điểm chung.
2. Nếu (P) // (Q) và a nằm trong (P) thì a // (Q) hoặc a nằm trong (Q).
3. Nếu a // b và (P) // (Q) thì góc giữa a và (P) bằng góc giữa b và (Q).
Có nhiều cách để chứng minh hai đường thẳng song song:
Có nhiều cách để chứng minh hai mặt phẳng song song:
Ví dụ 1: Cho hai đường thẳng a và b. Biết a có vectơ chỉ phương là u = (1, 2, 3) và b có vectơ chỉ phương là v = (2, 4, 6). Chứng minh a // b.
Giải: Vì v = 2u nên hai vectơ u và v cùng phương. Do đó, a // b.
Ví dụ 2: Cho hai mặt phẳng (P) và (Q). Biết (P) có vectơ pháp tuyến là n1 = (1, 0, 0) và (Q) có vectơ pháp tuyến là n2 = (2, 0, 0). Chứng minh (P) // (Q).
Giải: Vì n2 = 2n1 nên hai vectơ n1 và n2 cùng phương. Do đó, (P) // (Q).
Lý thuyết về đường thẳng và mặt phẳng song song là một phần quan trọng của Hình học không gian. Việc nắm vững các khái niệm, tính chất và điều kiện để chứng minh sự song song sẽ giúp học sinh giải quyết các bài toán một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích về chủ đề này.