Chào mừng bạn đến với bài học lý thuyết Hình lăng trụ và hình hộp, một phần quan trọng trong chương trình Toán 11 Cánh Diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về các hình khối không gian này.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, các yếu tố cơ bản và công thức tính toán liên quan đến hình lăng trụ và hình hộp. Mục tiêu là giúp bạn hiểu rõ bản chất và áp dụng kiến thức vào giải quyết các bài tập thực tế.
I. Hình lăng trụ
I. Hình lăng trụ
1. Định nghĩa
- Hình gồm hai đa giác \({A_1}{A_2}...{A_n}\), \({A_1}'{A_2}'...{A_n}'\) và các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\) được gọi là hình lăng trụ và kí hiệu là \({A_1}{A_2}...{A_n}.{A_1}'{A_2}'...{A_n}'\).
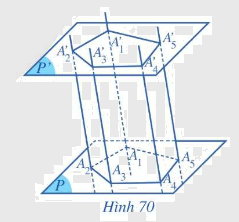
- Trong hình lăng trụ \({A_1}{A_2}...{A_n}.{A_1}'{A_2}'...{A_n}'\)
+ Các điểm \({A_1},{A_2},...,{A_n}\) và \({A_1}',{A_2}',...,{A_n}'\) được gọi là các đỉnh.
+ Các đoạn thẳng \({A_1}{A_1}',{A_2}{A_2}',...,{A_n}{A_n}'\) được gọi là các cạnh bên, các đoạn thẳng.\({A_1}{A_2},{A_2}{A_3},...,{A_n}{A_1}\)và \({A_1}'{A_2}',{A_2}'{A_3}',...,{A_n}'{A_1}'\) gọi là cạnh đáy của hình trụ.
+ Hai đa giác \({A_1}{A_2}...{A_n}\)và \({A_1}'{A_2}'...{A_n}'\) được gọi là hai mặt đáy của hình lăng trụ.
+ Các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\) gọi là các mặt bên của hình trụ.
* Chú ý: Nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác,… thì lăng trụ tương ứng gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác.
2. Tính chất
- Các cạnh bên của hình lăng trụ song song và bằng nhau.
- Các mặt bên của hình lăng trụ là các hình bình hành.
- Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.
II. Hình hộp
1. Định nghĩa
- Hình hộp là hình lăng trụ có đáy là hình bình hành.
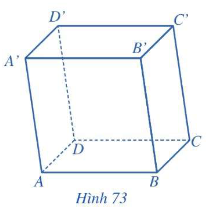
- Trong mỗi hình hộp, ta gọi:
+ Hai mặt không có đỉnh chung là hai mặt đối diện.
+ Hai cạnh song song không nằm trong một mặt phẳng là hai cạnh đối diện.
+ Hai đỉnh không thuộc cùng một mặt là hai đỉnh đối diện.
+ Đoạn thẳng nối hai đỉnh đối diện là đường chéo.
2. Tính chất
- Các mặt của hình hộp là hình bình hành.
- Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.
Hình lăng trụ và hình hộp là hai loại hình khối quan trọng trong chương trình Hình học không gian lớp 11. Việc nắm vững lý thuyết về hai hình này là nền tảng để giải quyết các bài toán liên quan đến thể tích, diện tích bề mặt và các tính chất khác.
Định nghĩa: Hình lăng trụ là hình đa diện được tạo bởi hai đáy là hai đa giác đồng dạng và các mặt bên là các hình bình hành.
Phân loại:
Công thức tính:
Định nghĩa: Hình hộp là hình đa diện được tạo bởi hai đáy là hai đa giác đồng dạng và các mặt bên là các hình bình hành.
Phân loại:
Công thức tính:
Hình hộp là một trường hợp đặc biệt của hình lăng trụ, trong đó đáy là hình bình hành. Do đó, tất cả các công thức tính toán của hình lăng trụ đều có thể áp dụng cho hình hộp.
Để hiểu rõ hơn về lý thuyết, chúng ta hãy xem xét một số bài tập vận dụng:
Khi giải các bài toán liên quan đến hình lăng trụ và hình hộp, cần chú ý đến các yếu tố sau:
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết Hình lăng trụ và hình hộp - SGK Toán 11 Cánh Diều. Chúc bạn học tập tốt!