Chào mừng bạn đến với bài giải Bài 3 trang 88 SGK Toán 11 tập 2 – Cánh Diều trên giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, chính xác, giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ bạn học Toán 11 hiệu quả nhất.
Cho tứ diện ABCD có (AB bot (BCD)), các tam giác BCD và ACD là những tam giác nhọn.
Đề bài
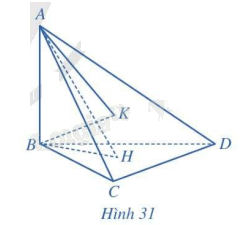
Cho tứ diện ABCD có \(AB \bot (BCD)\), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:
a) \(CD \bot (ABH)\)
b) \(CD \bot (ABK)\)
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm
Phương pháp giải - Xem chi tiết
Dựa vào điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh
Lời giải chi tiết
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)
c) Ta có: \( CD \bot \left( {ABH} \right)\) và \(CD \bot \left( {ABK} \right)\). Mà theo tính chất 1, chỉ có duy nhất 1 mặt phẳng đi qua A và B vuông góc với CD. Nên \(\left( {ABH} \right) \equiv \left( {ABK} \right)\).
Ta có H là trực tâm của tam giác BCD nên BH giao với CD tại 1 điểm I, K là trực tâm của tam giác ACD nên AK giao với CD tại 1 điểm I'.
Mà (ABHK) cắt CD tại 1 điểm thuộc CD.
Nên I và I' trùng nhau hay AK, BH, CD cùng đi qua một điểm.
Bài 3 trang 88 SGK Toán 11 tập 2 – Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm số hợp, và kỹ năng giải phương trình, bất phương trình.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải Bài 3 trang 88 SGK Toán 11 tập 2 – Cánh Diều, chúng ta cần thực hiện các bước sau:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Để tính đạo hàm của hàm số này, ta áp dụng quy tắc đạo hàm của lũy thừa:
f'(x) = 3x2 - 6x
Để tìm cực trị của hàm số, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
=> 3x(x - 2) = 0
=> x = 0 hoặc x = 2
Vậy hàm số có hai điểm cực trị tại x = 0 và x = 2.
Ngoài việc giải Bài 3 trang 88 SGK Toán 11 tập 2 – Cánh Diều, bạn nên luyện tập thêm các bài tập tương tự để nắm vững kiến thức về đạo hàm. Bạn cũng có thể tham khảo các tài liệu học tập khác, như sách bài tập, đề thi thử, và các trang web học toán online.
Khi giải các bài toán về đạo hàm, bạn cần chú ý đến các quy tắc đạo hàm cơ bản, quy tắc tính đạo hàm của hàm số hợp, và kỹ năng giải phương trình, bất phương trình. Bạn cũng nên kiểm tra lại kết quả của mình để đảm bảo tính chính xác.
| Hàm số | Đạo hàm |
|---|---|
| y = c (c là hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |
Hy vọng bài giải Bài 3 trang 88 SGK Toán 11 tập 2 – Cánh Diều trên giaitoan.edu.vn sẽ giúp bạn học Toán 11 hiệu quả hơn. Chúc bạn thành công!