Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 5 trang 38 SGK Toán 11 tập 1 - Cánh Diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m (Hình 37)
Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = -1 (Hình 37)
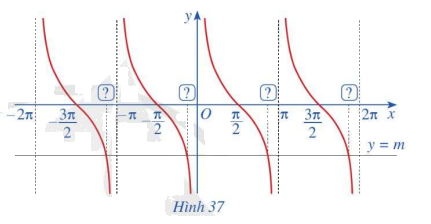
a) Từ hoành độ giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m trên khoảng \(\left( {0;\pi } \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.
b) Có nhận xét gì về nghiệm của phương trình cotx = -1?
Phương pháp giải:
Dựa vào phương trình lượng giác của sinx và cosx để làm bài:
Lời giải chi tiết:
a) Do hoành độ giao điểm nằm trên khoảng \(\left( {0;\pi } \right)\) nên: \(\cot x = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng \(\left( {0;\pi } \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
a) Giải phương trình \(\cot x = 1\)
b) Tìm góc lượng giác x sao cho \(\cot x = \cot \left( { - {{83}^ \circ }} \right)\)
Phương pháp giải:
Sử dụng công thức tổng quát để giải phương trình cot
Lời giải chi tiết:
a) \(\cot x = 1 \Leftrightarrow \cot x = \cot \frac{\pi }{4} \Leftrightarrow x = \frac{\pi }{4} + k\pi \)
b) \(\cot x = \cot \left( { - {{83}^ \circ }} \right) \Leftrightarrow x = - {83^ \circ } + k{.180^ \circ }\)
Mục 5 trang 38 SGK Toán 11 tập 1 - Cánh Diều tập trung vào việc vận dụng các kiến thức về phép biến hình affine để giải quyết các bài toán hình học phẳng. Các bài tập trong mục này thường yêu cầu học sinh xác định phép biến hình affine, tìm ảnh của một điểm, một đường thẳng hoặc một hình qua phép biến hình affine, và chứng minh các tính chất liên quan đến phép biến hình affine.
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 5 trang 38 SGK Toán 11 tập 1 - Cánh Diều, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh xác định một phép biến hình affine dựa trên các thông tin cho trước, chẳng hạn như ảnh của một số điểm hoặc đường thẳng. Để giải bài tập này, học sinh cần nắm vững định nghĩa và các tính chất của phép biến hình affine, cũng như biết cách sử dụng các công thức liên quan.
Bài tập này yêu cầu học sinh tìm tọa độ của ảnh của một điểm qua một phép biến hình affine cho trước. Để giải bài tập này, học sinh cần áp dụng công thức biến đổi tọa độ của phép biến hình affine.
Bài tập này yêu cầu học sinh tìm phương trình của ảnh của một đường thẳng qua một phép biến hình affine cho trước. Để giải bài tập này, học sinh cần tìm ảnh của hai điểm bất kỳ trên đường thẳng, sau đó xác định phương trình đường thẳng đi qua hai điểm này.
Bài tập này yêu cầu học sinh chứng minh các tính chất liên quan đến phép biến hình affine, chẳng hạn như tính chất bảo toàn tính thẳng hàng, tính chất bảo toàn tỷ số độ dài, và tính chất bảo toàn diện tích. Để giải bài tập này, học sinh cần sử dụng định nghĩa và các tính chất của phép biến hình affine, cũng như các kiến thức về hình học phẳng.
Để giải các bài tập về phép biến hình affine một cách hiệu quả, học sinh cần:
Ví dụ 1: Cho phép biến hình affine f xác định bởi f(x, y) = (2x + y, x - y). Tìm ảnh của điểm A(1, 2) qua phép biến hình f.
Giải: Áp dụng công thức biến đổi tọa độ của phép biến hình f, ta có:
f(1, 2) = (2(1) + 2, 1 - 2) = (4, -1)
Vậy ảnh của điểm A(1, 2) qua phép biến hình f là điểm A'(4, -1).
Để củng cố kiến thức và kỹ năng giải bài tập về phép biến hình affine, các em học sinh có thể tự giải thêm các bài tập sau:
Hy vọng rằng với những kiến thức và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập về phép biến hình affine trong SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt!