Bài 5 trang 94 SGK Toán 11 tập 1 thuộc chương trình Toán 11 Cánh Diều, tập trung vào việc giải các bài toán liên quan đến phép biến hóa lượng giác. Bài tập này đòi hỏi học sinh nắm vững kiến thức về công thức lượng giác cơ bản và kỹ năng biến đổi đại số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\) a) Xác định giao điểm của MN với mặt phẳng (ABC) b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)
Đề bài
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\)
a) Xác định giao điểm của MN với mặt phẳng (ABC)
b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)
Phương pháp giải - Xem chi tiết
a) Muốn tìm giao điểm của một đường thẳng a và mặt phẳng (P), ta tìm giao điểm của a và một đường thẳng b nằm trong (P):
\(\left\{ \begin{array}{l}a \cap b = M\\b \subset (P)\end{array} \right. \Rightarrow M = a \cap (P)\)
Bước 1: Xác định mp (Q) chứa a
Bước 2: Tìm giao tuyến \(b = (P) \cap (Q)\)
Bước 3: Trong \((Q):a \cap b = M\) mà \(b \subset (P)\)suy ra \(M = a \cap (P)\)
b) Để xác định giao tuyến của hai mặt phẳng, ta tìm điểm chung của chúng.
b, Đường thẳng đi qua hai điểm chung là giao tuyến
Lời giải chi tiết
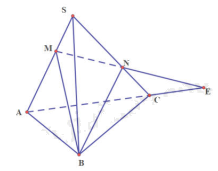
a) Tam giác SAC có: MN cắt AC tại E mà AC thuộc mp (ABC)
Do đó: E là giao điểm của MN và (ABC)
b) Ta có: B thuộc hai mặt phẳng (BMN) và (ABC)
E thuộc hai mặt phẳng (BMN) và (ABC)
Suy ra: BE là giao tuyến của hai mặt phẳng (BMN) và (ABC)
Bài 5 trang 94 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về phép biến hóa lượng giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các công thức lượng giác cơ bản, kỹ năng biến đổi đại số và khả năng áp dụng kiến thức vào thực tế.
Bài 5 yêu cầu học sinh giải các phương trình lượng giác. Các phương trình này thường có dạng phức tạp, đòi hỏi học sinh phải sử dụng các kỹ thuật biến đổi lượng giác để đưa về dạng đơn giản hơn. Cụ thể, bài tập có thể yêu cầu:
Để giải Bài 5 trang 94 SGK Toán 11 tập 1 - Cánh Diều, học sinh có thể áp dụng các phương pháp sau:
Ví dụ 1: Giải phương trình sin x = 1/2
Lời giải:
Phương trình sin x = 1/2 có nghiệm là:
Trong đó k là số nguyên.
Ví dụ 2: Giải phương trình cos 2x = 0
Lời giải:
Phương trình cos 2x = 0 có nghiệm là:
Trong đó k là số nguyên.
Khi giải Bài 5 trang 94 SGK Toán 11 tập 1 - Cánh Diều, học sinh cần lưu ý những điều sau:
Học sinh có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về phép biến hóa lượng giác:
Bài 5 trang 94 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng, giúp học sinh củng cố kiến thức về phép biến hóa lượng giác. Bằng cách nắm vững các công thức lượng giác cơ bản, kỹ năng biến đổi đại số và luyện tập thường xuyên, học sinh có thể giải bài tập này một cách hiệu quả và đạt kết quả tốt trong học tập.