Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2, trang 97, 98, 99 và 100 sách giáo khoa Toán 11 tập 1 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Trong không gian, cho điểm M và đường thẳng d không đi qua điểm M (Hình 36). Nêu dự đoán về số đường thẳng đi qua điểm M và song song với đường thẳng d.
Trong không gian, cho điểm M và đường thẳng d không đi qua điểm M (Hình 36). Nêu dự đoán về số đường thẳng đi qua điểm M và song song với đường thẳng d.
Phương pháp giải:
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho
Lời giải chi tiết:
Có một và chỉ một đường thẳng đi qua điểm M và song song với đường thẳng d
Cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó \(a = (P) \cap (R),b = (Q) \cap (R),c = (P) \cap (Q)\)
- Nếu hai đường thẳng a và b cắt nhau tại điểm M thì đường thẳng c có đi qua điểm M hay không (Hình 38a)?
- Nếu đường thẳng a song song với đường thẳng b thì đường thẳng a có song song với đường thẳng c hay không (Hình 38b)?

Phương pháp giải:
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy đồng quy hoặc đôi một song song với nhau.
Lời giải chi tiết:
- Nếu hai đường thẳng a và b cắt nhau tại điểm M thì đường thẳng c đi qua điểm M
- Nếu đường thẳng a song song với đường thẳng b thì đường thẳng a song song với đường thẳng c
Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAD) và (SBC).
Phương pháp giải:
Để xác định giao tuyến của hai mặt phẳng, ta tìm điểm chung của chúng.
Đường thẳng đi qua hai điểm chung là giao tuyến
Lời giải chi tiết:

Ta có: AB thuộc (SAB)
CD thuộc (SCD)
Mà AB // CD, S là giao điểm của hai mặt phẳng (SAB) và (SCD)
Từ S kẻ Sx sao cho Sx // AB // CD
Vậy Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD)
Chứng minh tương tự, ta có: Sy là giao tuyến của hai mặt phẳng (SAD) và (SBC).
Trong mặt phẳng, hãy nêu vị trí tương đối của hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba.
Phương pháp giải:
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
Lời giải chi tiết:
Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau
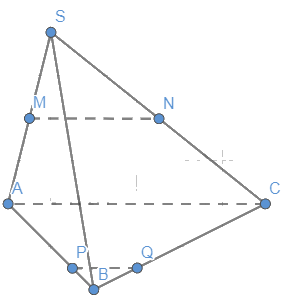
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của các đoạn thẳng SA, SC. Lấy các điểm P, Q lần lượt thuộc các đoạn thẳng AB, BC sao cho \(\frac{{BP}}{{BA}} = \frac{{BQ}}{{BC}} = \frac{1}{3}\). Chứng minh rằng MN song song với PQ.
Phương pháp giải:
- Nếu ba mp phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc song song với nhau
- Hệ quả: Nếu hai mp phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó
- Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau
\(\left\{ \begin{array}{l}a \ne b\\a//c\\b//c\end{array} \right. \Rightarrow a//b\)
Lời giải chi tiết:

Ta có M, N lần lượt là trung điểm của SA, SC
Do đó, tam giác SAC có MN // AC (1)
Ta có: \(\frac{{BP}}{{BA}} = \frac{{BQ}}{{BC}} = \frac{1}{3}\)
Suy ra: PQ // AC (2)
Từ (1) và (2), suy ra: MN // PQ
Mục 2 của SGK Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức về phép biến hình. Cụ thể, các em sẽ được làm quen với các khái niệm như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để học tập các kiến thức tiếp theo trong chương trình Toán 11.
Các bài tập trên trang 97 chủ yếu xoay quanh việc xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép tịnh tiến. Để giải các bài tập này, các em cần nắm vững công thức của phép tịnh tiến: x' = x + a, y' = y + b, trong đó (a, b) là vectơ tịnh tiến.
Phép quay là một phép biến hình quan trọng trong hình học. Các bài tập trên trang 98 yêu cầu các em xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép quay. Để giải các bài tập này, các em cần nắm vững công thức của phép quay quanh gốc tọa độ O(0; 0) với góc quay α:
x' = x cos α - y sin α
y' = x sin α + y cos α
Phép đối xứng trục là phép biến hình biến mỗi điểm thành điểm đối xứng của nó qua một trục cho trước. Các bài tập trên trang 99 yêu cầu các em xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép đối xứng trục.
Phép đối xứng tâm là phép biến hình biến mỗi điểm thành điểm đối xứng của nó qua một tâm cho trước. Các bài tập trên trang 100 yêu cầu các em xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép đối xứng tâm.
Để giải các bài tập về phép biến hình một cách hiệu quả, các em cần:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn khi giải các bài tập trong mục 2, trang 97, 98, 99, 100 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt!