Chào mừng bạn đến với bài học về Lý thuyết Phép tính Lôgarit trong chương trình Toán 11 Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về lôgarit, giúp bạn giải quyết các bài toán một cách hiệu quả.
Chúng tôi sẽ trình bày một cách rõ ràng, dễ hiểu các định nghĩa, tính chất và ứng dụng của phép tính lôgarit, đồng thời cung cấp các ví dụ minh họa cụ thể.
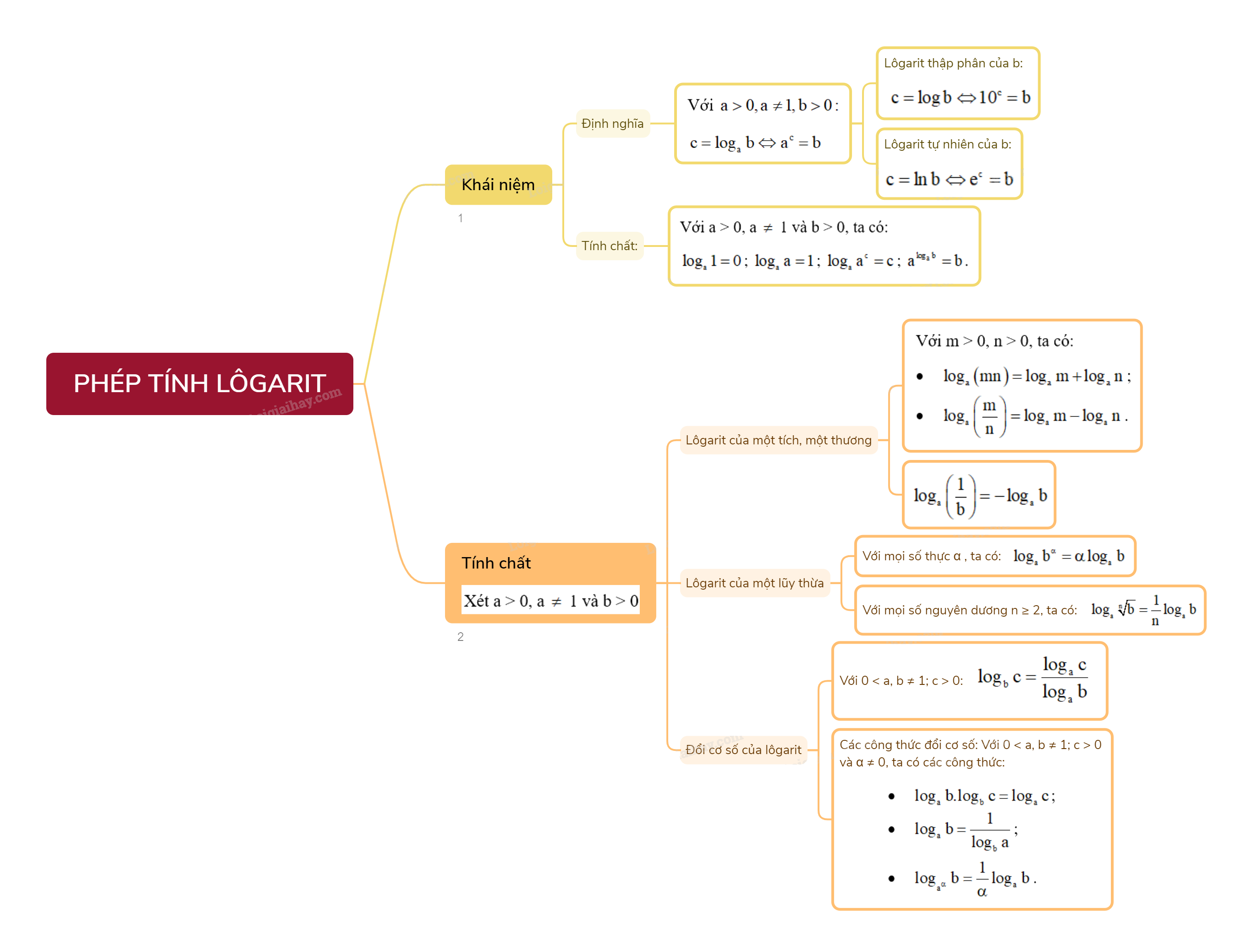
1. Khái niệm lôgarit a) Định nghĩa
1. Khái niệm lôgarit
a) Định nghĩa
Với a > 0, a \( \ne \) 1 và b > 0, ta có: \(c = {\log _a}b \Leftrightarrow {a^c} = b\). Ngoài ra:
- Lôgarit thập phân của b là lôgarit cơ số 10 của số thực dương b:
\(c = \log b \Leftrightarrow {10^c} = b\)
- Lôgarit tự nhiên của b là lôgarit cơ số e của số thực dương b:
\(c = \ln b \Leftrightarrow {e^c} = b\).
b) Tính chất
Với a > 0, a \( \ne \) 1 và b > 0, ta có:
\({\log _a}1 = 0\); \({\log _a}a = 1\); \({\log _a}{a^c} = c\); \({a^{{{\log }_a}b}} = b\).
2. Một số tính chất của phép tính lôgarit
Trong mục này, ta xét a > 0, a \( \ne \) 1 và b > 0.
a) Lôgarit của một tích, một thương
Với m > 0, n > 0, ta có:
Nhận xét: \({\log _a}\left( {\frac{1}{b}} \right) = - {\log _a}b\).
b) Lôgarit của một lũy thừa
Với mọi số thực \(\alpha \), ta có: \({\log _a}{b^\alpha } = \alpha {\log _a}b\).
Nhận xét: Với mọi số nguyên dương \(n \ge 2\), ta có: \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\).
c) Đổi cơ số của lôgarit
Với a, b là hai số thực dương khác 1 và c là số thực dương, ta có: \({\log _b}c = \frac{{{{\log }_a}c}}{{{{\log }_a}b}}\).
Nhận xét: Với a, b là hai số thực dương khác 1, c > 0 và \(\alpha \ne 0\), ta có những công thức sau:
Phép tính lôgarit là một trong những chủ đề quan trọng trong chương trình Toán 11, đặc biệt là với sách giáo khoa Cánh diều. Hiểu rõ lý thuyết là nền tảng để giải quyết các bài toán liên quan một cách chính xác và hiệu quả. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết phép tính lôgarit, bao gồm định nghĩa, tính chất, các dạng bài tập thường gặp và cách giải.
Lôgarit của một số dương b (với b ≠ 1) cơ số a (với a > 0 và a ≠ 1) là số x sao cho ax = b. Ký hiệu: x = logab.
Dưới đây là một số tính chất quan trọng của lôgarit mà bạn cần nắm vững:
Các bài tập về phép tính lôgarit thường xoay quanh các chủ đề sau:
Ví dụ 1: Tính log28.
Giải: Vì 23 = 8, nên log28 = 3.
Ví dụ 2: Rút gọn biểu thức log39 + log33.
Giải: Sử dụng tính chất loga(xy) = logax + logay, ta có:
log39 + log33 = log3(9*3) = log327 = 3.
Ví dụ 3: Giải phương trình log2(x + 1) = 3.
Giải: x + 1 = 23 = 8 => x = 7.
Khi làm bài tập về lôgarit, bạn cần lưu ý những điều sau:
Lôgarit có nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết phép tính lôgarit - Toán 11 Cánh diều. Chúc bạn học tập tốt!