Bài 3 trang 94 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Cánh diều, tập trung vào việc giải các bài toán liên quan đến đạo hàm của hàm số. Bài tập này đòi hỏi học sinh nắm vững kiến thức về các quy tắc tính đạo hàm và ứng dụng chúng vào giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang
Đề bài
Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là 100%, tương ứng với góc \({90^ \circ }\) (độ dốc 10% tương ứng với góc \({9^ \circ }\)). Giả sử có hai điểm \(A,B\) nằm ở độ cao lần lượt là 200 m, 220 m so với mực nước biển và đoạn dốc \(AB\) dài 120 m. Độ dốc đó bằng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm?
Phương pháp giải - Xem chi tiết
‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
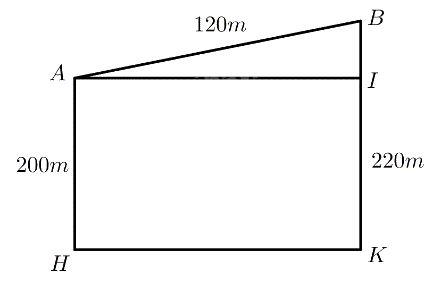
Mô hình hoá như hình vẽ, với \(AB\) là chiều dài con dốc, \(AH\) là độ cao của điểm \(A\) so với mặt nước biển, \(BK\) là độ cao của điểm \(B\) so với mặt nước biển, \(BI\) là chiều cao của con dốc, độ lớn của góc \(\widehat {BAI}\) chỉ độ dốc.
Ta có: \(AH = 200,BK = 220,AB = 120\).
\(AHKB\) là hình chữ nhật \( \Rightarrow IK = AH = 200 \Rightarrow BI = BK - IK = 220 - 200 = 20\)
Vì tam giác \(ABI\) vuông tại \(I\) nên ta có:
\(\sin \widehat {ABI} = \frac{{BI}}{{AB}} = \frac{{20}}{{120}} = \frac{1}{6} \Rightarrow \widehat {ABI} \approx 9,{59^ \circ }\) tương ứng với 10,66%
Vậy độ dốc của con dốc đó là 10,66%.
Bài 3 trang 94 SGK Toán 11 tập 2 - Cánh diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 3 yêu cầu học sinh tính đạo hàm của các hàm số được cho. Các hàm số này có thể bao gồm các hàm số đơn giản như đa thức, hàm lượng giác, hàm mũ, hàm logarit, hoặc các hàm số phức tạp hơn được tạo thành từ các hàm số đơn giản thông qua các phép toán cộng, trừ, nhân, chia, và hợp thành.
Để giải bài tập này, học sinh cần nắm vững các quy tắc tính đạo hàm cơ bản, bao gồm:
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể. Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = 2x3 + sin x - ex.
Áp dụng các quy tắc đạo hàm đã nêu, ta có:
f'(x) = (2x3)' + (sin x)' - (ex)' = 6x2 + cos x - ex
Ngoài việc tính đạo hàm của các hàm số đơn giản, bài tập Bài 3 trang 94 SGK Toán 11 tập 2 - Cánh diều còn có thể yêu cầu học sinh:
Để giải bài tập này một cách hiệu quả, học sinh nên:
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự trong SGK Toán 11 tập 2 - Cánh diều hoặc các đề thi thử Toán 11.
Bài 3 trang 94 SGK Toán 11 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng của nó. Bằng cách nắm vững các quy tắc đạo hàm cơ bản và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong các kỳ thi.
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập này, các em học sinh sẽ hiểu rõ hơn về đạo hàm và ứng dụng của nó trong chương trình Toán 11.