Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 2 trang 81 SGK Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d
Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d, a, b; sàn nhà coi như mặt phẳng (P) chứa a và b. Hỏi đường thẳng d có vuông góc với mặt phẳng (P) hay không?
Phương pháp giải:
Quan sát hình vẽ để dự đoán
Lời giải chi tiết:
Đường thẳng d có vuông góc với mặt phẳng (P)
Vì: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b\end{array} \right. \Rightarrow d \bot \left( P \right)\)
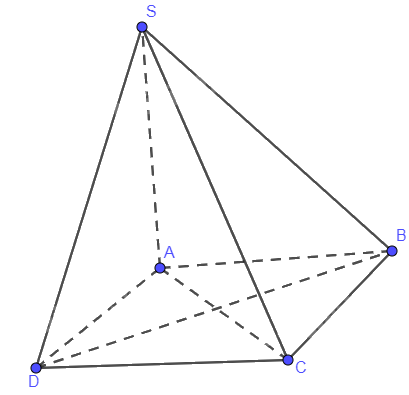
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, \(SA \bot \left( {ABCD} \right)\). Chứng minh rằng \(BD \bot \left( {SAC} \right)\)
Phương pháp giải:
Dựa vào lý thuyết vừa học để chứng minh
Lời giải chi tiết:

Do ABCD là hình thoi
=> AC vuông góc với BD
+ SA vuông góc (ABCD)
=> SA vuông góc với BD
Xét (SAC) có:
+ AC vuông góc với BD
+ SA vuông góc với BD
=> BD vuông góc với (SAC)
Mục 2 trang 81 SGK Toán 11 tập 2 - Cánh Diều tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế, đặc biệt là các bài toán liên quan đến khảo sát hàm số. Các bài tập trong mục này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản, các quy tắc tính đạo hàm và kỹ năng phân tích bài toán để lựa chọn phương pháp giải phù hợp.
Mục 2 bao gồm một số bài tập với các mức độ khó khác nhau, từ dễ đến khó. Dưới đây là nội dung chi tiết giải các bài tập chính:
Bài tập này yêu cầu học sinh tìm đạo hàm của các hàm số đơn giản, ví dụ như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit. Để giải bài tập này, học sinh cần áp dụng các công thức đạo hàm cơ bản và các quy tắc tính đạo hàm.
Ví dụ: Tìm đạo hàm của hàm số y = x2 + 2x - 1.
Lời giải: y' = 2x + 2.
Bài tập này yêu cầu học sinh tính đạo hàm cấp hai của các hàm số. Để giải bài tập này, học sinh cần tính đạo hàm cấp một trước, sau đó tính đạo hàm của đạo hàm cấp một.
Ví dụ: Tính đạo hàm cấp hai của hàm số y = x3.
Lời giải: y' = 3x2, y'' = 6x.
Bài tập này yêu cầu học sinh khảo sát hàm số bằng đạo hàm, bao gồm việc tìm khoảng đồng biến, khoảng nghịch biến, cực trị và điểm uốn. Để giải bài tập này, học sinh cần tìm đạo hàm cấp một và đạo hàm cấp hai, sau đó phân tích dấu của đạo hàm để xác định các khoảng đồng biến, khoảng nghịch biến, cực trị và điểm uốn.
Ví dụ: Khảo sát hàm số y = x3 - 3x2 + 2.
Lời giải:
Bài tập này yêu cầu học sinh ứng dụng đạo hàm để giải quyết các bài toán thực tế, ví dụ như bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, bài toán tối ưu hóa. Để giải bài tập này, học sinh cần xây dựng hàm số mô tả bài toán, sau đó tìm đạo hàm và giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị. Cuối cùng, so sánh các giá trị của hàm số tại các điểm cực trị và các điểm biên để tìm giá trị lớn nhất, giá trị nhỏ nhất.
Khi giải các bài tập trong mục 2 trang 81 SGK Toán 11 tập 2 - Cánh Diều, học sinh cần lưu ý một số điểm sau:
Hy vọng rằng với những hướng dẫn chi tiết trên, bạn đã có thể giải quyết thành công các bài tập trong mục 2 trang 81 SGK Toán 11 tập 2 - Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!