Bài viết này cung cấp đầy đủ lý thuyết về định nghĩa đạo hàm và ý nghĩa hình học của đạo hàm trong chương trình Toán 11 Cánh diều. Chúng tôi trình bày một cách dễ hiểu, kèm theo ví dụ minh họa để bạn có thể nắm bắt kiến thức một cách nhanh chóng và hiệu quả.
Học toán online tại giaitoan.edu.vn, bạn sẽ được tiếp cận với phương pháp học tập hiện đại, tài liệu chất lượng và đội ngũ giáo viên giàu kinh nghiệm.
1. Định nghĩa - Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) và điểm \({x_0} \in \left( {a;b} \right)\).
1. Định nghĩa
- Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) và điểm \({x_0} \in \left( {a;b} \right)\).
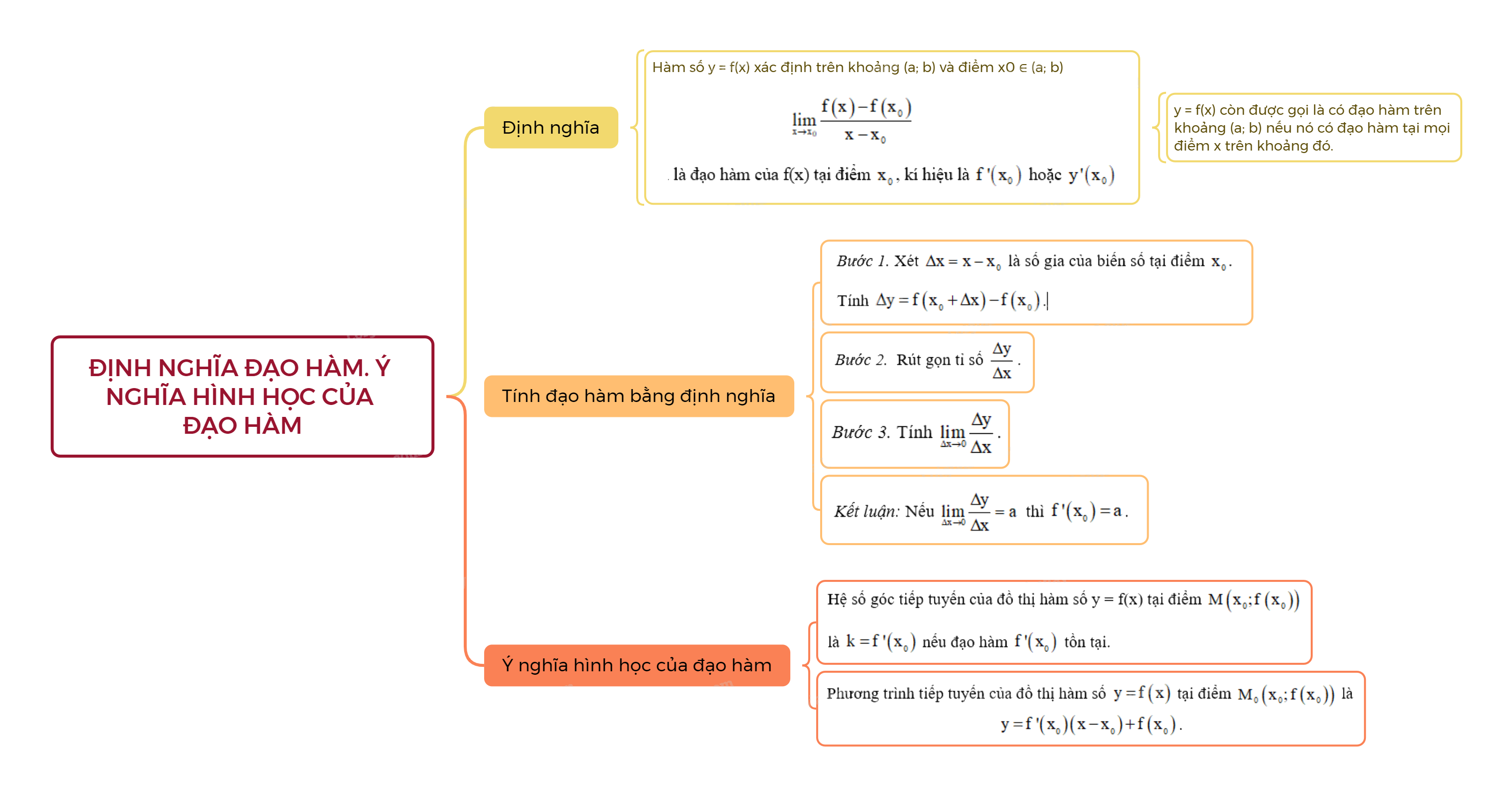
Nếu tồn tại giới hạn hữu hạn \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) thì giới hạn đó được gọi là đạo hàm của hàm số \(y = f\left( x \right)\)tại \({x_0}\) và được kí hiệu là \(f'\left( {{x_0}} \right)\) hoặc \(y{'_{x_o}}\).
- Hàm số \(y = f\left( x \right)\) được gọi là có đạo hàm trên khoảng (a; b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.
2. Cách tính đạo hàm bằng định nghĩa
Để tính đạo hàm \(f'\left( {{x_0}} \right)\) của hàm số \(y = f\left( x \right)\) tại \({x_0}\), ta lần lượt thực hiện ba bước sau:
Bước 1. Xét \(\Delta x = x - {x_0}\) là số gia của biến số tại điểm \({x_0}\).
Tính \(\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\).
Bước 2. Rút gọn tỉ số \(\frac{{\Delta y}}{{\Delta x}}\).
Bước 3. Tính \(\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}\).
Kết luận: Nếu \(\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = a\) thì \(f'\left( {{x_0}} \right) = a\).
3. Ý nghĩa hình học của đạo hàm
- Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \({x_0}\) là hệ số góc của tiếp tuyến của đồ thị hàm số đó tại điểm \({M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)\).
- Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \({M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).
Đạo hàm là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu sự thay đổi của hàm số. Trong chương trình Toán 11 Cánh diều, học sinh sẽ được làm quen với định nghĩa đạo hàm và ý nghĩa hình học của nó.
Cho hàm số y = f(x) xác định trên khoảng (a; b). Nếu tồn tại giới hạn:
limΔx→0 [f(x + Δx) - f(x)] / Δx
thì hàm số f(x) được gọi là khả vi tại điểm x và giới hạn trên được gọi là đạo hàm của hàm số f(x) tại điểm x, ký hiệu là f'(x).
f'(x) = limΔx→0 [f(x + Δx) - f(x)] / Δx
Lưu ý:
Đạo hàm f'(x) của hàm số y = f(x) tại điểm x0 là hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm (x0; f(x0)).
Tiếp tuyến của đồ thị hàm số tại một điểm là đường thẳng đi qua điểm đó và có hệ số góc bằng đạo hàm của hàm số tại điểm đó.
Để tính đạo hàm một cách nhanh chóng và hiệu quả, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x2 + 3x - 2
f'(x) = (x2)' + (3x)' - (2)' = 2x + 3 - 0 = 2x + 3
Ví dụ 2: Tìm hệ số góc của tiếp tuyến của đồ thị hàm số y = x3 - 2x + 1 tại điểm có hoành độ x = 1
y' = (x3)' - (2x)' + (1)' = 3x2 - 2
Tại x = 1, y' = 3(1)2 - 2 = 1. Vậy hệ số góc của tiếp tuyến là 1.
Hãy tự giải các bài tập sau để củng cố kiến thức:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết định nghĩa đạo hàm và ý nghĩa hình học của đạo hàm trong chương trình Toán 11 Cánh diều. Chúc bạn học tập tốt!