Chào mừng bạn đến với bài học về Lý thuyết Hai mặt phẳng song song trong chương trình Toán 11 Cánh Diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hai mặt phẳng song song, giúp bạn giải quyết các bài tập một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, điều kiện nhận biết hai mặt phẳng song song, các tính chất và ứng dụng của lý thuyết này trong hình học không gian.
I. Hai mặt phẳng song song
I. Hai mặt phẳng song song
Hai mặt \(\left( P \right)\) và \(\left( Q \right)\) được gọi là song song với nhau nếu chúng không có điểm chung. Kí hiệu\(\left( P \right)\)// \(\left( Q \right)\) hay \(\left( Q \right)\)//\(\left( P \right)\).
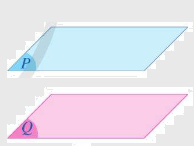
*Nhận xét: Hai mặt \(\left( P \right)\) và \(\left( Q \right)\) có diểm chung. Khi đó, chúng cắt nhau theo một đường thẳng.
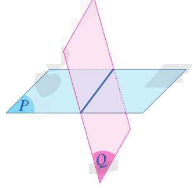
II. Điều kiện và tính chất
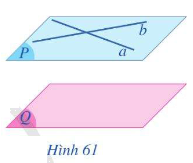
* Hệ quả:
- Nếu đường thẳng a song song với mặt phẳng \(\left( Q \right)\) thì có duy nhất một mặt phẳng chứa a và song song với mặt phẳng \(\left( Q \right)\)
- Nếu 2 mặt phẳng phân biệt cùng song song với mặt phẳng thứ 3 thì song song với nhau.
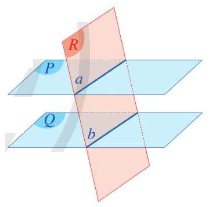
III. Định lí Thalès
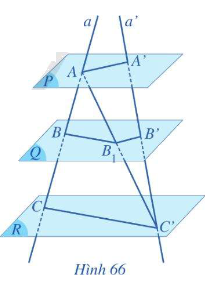
Nếu a, b là hai cát tuyến bất kì cắt 3 mặt phẳng song song \(\left( P \right)\) , \(\left( Q \right)\)và\(\left( R \right)\) lần lượt tại các điểm A, B, C và A’, B’, C’ thì
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\)
Trong chương trình Hình học không gian lớp 11, kiến thức về hai mặt phẳng song song đóng vai trò then chốt. Việc nắm vững lý thuyết này không chỉ giúp học sinh hiểu sâu sắc hơn về không gian ba chiều mà còn là nền tảng để giải quyết các bài toán phức tạp hơn.
Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung. Ký hiệu: (P) // (Q). Điều này có nghĩa là khi kéo dài vô hạn, hai mặt phẳng này sẽ không giao nhau tại bất kỳ điểm nào.
Có một số điều kiện để nhận biết hai mặt phẳng song song:
Hai mặt phẳng song song có những tính chất quan trọng sau:
Lý thuyết hai mặt phẳng song song được ứng dụng rộng rãi trong việc giải các bài toán về hình học không gian, đặc biệt là:
Bài tập 1: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng mặt phẳng (SAM) song song với mặt phẳng (BCD).
Hướng dẫn: Chứng minh SM song song với BD và AM song song với CD. Từ đó suy ra (SAM) // (BCD).
Bài tập 2: Cho hai mặt phẳng (P) và (Q) song song với nhau. Trên (P) có điểm A và trên (Q) có điểm B. Tìm quỹ tích của trung điểm I của đoạn AB.
Hướng dẫn: Gọi C là hình chiếu vuông góc của A lên (Q). Khi đó, I là trung điểm của AC. Do đó, I thuộc mặt phẳng trung bình của (P) và (Q).
Để hiểu sâu hơn về lý thuyết hai mặt phẳng song song, bạn có thể tìm hiểu thêm về:
Lý thuyết Hai mặt phẳng song song là một phần quan trọng trong chương trình Hình học không gian lớp 11. Việc nắm vững lý thuyết này sẽ giúp bạn tự tin hơn khi giải các bài toán và hiểu sâu sắc hơn về không gian ba chiều. Hãy luyện tập thường xuyên và áp dụng lý thuyết vào thực tế để đạt được kết quả tốt nhất.