Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 89 và 90 sách giáo khoa Toán 11 tập 2, chương trình Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Quan sát Hình 32 và cho biết: a) Hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng nào;
Quan sát Hình 32 và cho biết:
a) Hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng nào;
b) Góc giữa đường thẳng \(MO\) và hình chiếu của đường thẳng đó trên mặt phẳng \(\left( P \right)\) là góc nào.
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Vì \(MH \bot \left( P \right),O \in \left( P \right)\) nên hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng \(HO\)
b) Góc giữa đường thẳng \(MO\) và hình chiếu của đường thẳng đó trên mặt phẳng \(\left( P \right)\) là góc \(\widehat {MOH}\).
Giả sử ở những giây đầu tiên sau khi cất cánh. máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc \({20^ \circ }\) và có vận tốc 200 km/h. Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 2 giây (làm tròn kết quả đến hàng phần mười).
Phương pháp giải:
Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết:
Đổi \(200km/h = \frac{{500}}{9}m/s\)
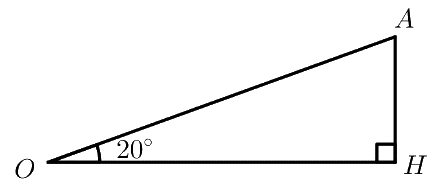
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.
Mục 1 trang 89, 90 SGK Toán 11 tập 2 - Cánh Diều tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về đồ thị hàm số lượng giác, phương trình lượng giác, và các ứng dụng thực tế của hàm số lượng giác để giải quyết các bài toán cụ thể.
Bài 1 thường bao gồm các câu hỏi trắc nghiệm và bài tập tự luận về các khái niệm cơ bản của hàm số lượng giác như tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, và các phép biến đổi đồ thị. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn.
Bài 2 tập trung vào việc giải các phương trình lượng giác cơ bản như sin(x) = a, cos(x) = a, tan(x) = a, cot(x) = a, với a là một số thực. Học sinh cần nắm vững các công thức lượng giác cơ bản và các phương pháp giải phương trình lượng giác như phương pháp đặt ẩn phụ, phương pháp sử dụng công thức biến đổi góc, và phương pháp sử dụng đường tròn lượng giác.
Bài 3 thường đưa ra các bài toán ứng dụng thực tế liên quan đến hàm số lượng giác, ví dụ như tính chiều cao của một tòa nhà, tính khoảng cách giữa hai điểm, hoặc mô tả các hiện tượng vật lý như dao động điều hòa. Việc giải các bài toán này đòi hỏi học sinh phải có khả năng phân tích bài toán, xây dựng mô hình toán học, và sử dụng các kiến thức về hàm số lượng giác để giải quyết.
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 89, 90 SGK Toán 11 tập 2 - Cánh Diều:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:
Hy vọng rằng với hướng dẫn giải chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 89, 90 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt!