Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4 trang 70, 71, 72 sách giáo khoa Toán 11 tập 1 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hàm số \(f\left( x \right) = x\) có đồ thị như ở Hình 9. Quan sát đồ thị đó và cho biết: a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới đâu. b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần đâu.
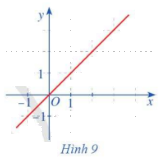
Cho hàm số \(f\left( x \right) = x\) có đồ thị như ở Hình 9. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới đâu.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần đâu.
Phương pháp giải:
Quan sát đồ thị hình 9 để trả lời câu hỏi.
Lời giải chi tiết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới dương vô cực.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần âm vô cực.
Tính: \(\mathop {\lim }\limits_{x \to - \infty } {x^4}.\)
Phương pháp giải:
\(\mathop {\lim }\limits_{x \to - \infty } {x^k} = + \infty \) với k là số nguyên dương chẵn.
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to - \infty } {x^4} = + \infty \)
Mục 4 của chương trình Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức về vectơ trong không gian. Các bài tập trong trang 70, 71, 72 SGK yêu cầu học sinh vận dụng các định nghĩa, tính chất của vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực) và các ứng dụng của vectơ trong việc giải quyết các bài toán hình học không gian.
Bài tập này yêu cầu học sinh xác định vectơ chỉ phương và vectơ pháp tuyến của một đường thẳng cho trước. Để làm được điều này, học sinh cần nắm vững định nghĩa của vectơ chỉ phương và vectơ pháp tuyến, cũng như các phương pháp tìm vectơ trong không gian.
Bài tập này yêu cầu học sinh lập phương trình của một đường thẳng khi biết các yếu tố như một điểm thuộc đường thẳng và một vectơ chỉ phương, hoặc hai điểm thuộc đường thẳng.
Bài tập này yêu cầu học sinh xác định vị trí tương đối của hai đường thẳng trong không gian (đồng phẳng, song song, cắt nhau, chéo nhau). Để làm được điều này, học sinh cần sử dụng các kiến thức về vectơ chỉ phương, vectơ nối hai điểm thuộc hai đường thẳng và tích hỗn hợp.
Các bước thực hiện:
Bài tập này yêu cầu học sinh tính góc giữa hai đường thẳng trong không gian. Để làm được điều này, học sinh cần sử dụng công thức tính góc giữa hai vectơ.
Công thức: cos(θ) = |a.b| / (||a|| * ||b||), trong đó a và b là các vectơ chỉ phương của hai đường thẳng.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải các bài tập trong mục 4 trang 70, 71, 72 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao!