Bài học này cung cấp kiến thức nền tảng về các số đặc trưng đo xu thế trung tâm, bao gồm trung bình cộng, trung vị và mốt, áp dụng cho mẫu số liệu ghép nhóm trong chương trình Toán 11 Cánh diều.
Chúng ta sẽ cùng tìm hiểu cách tính toán và ý nghĩa của từng số đặc trưng này, cũng như cách sử dụng chúng để phân tích và so sánh các bộ dữ liệu khác nhau.
Nội dung được trình bày một cách dễ hiểu, có ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức.
1. Mẫu số liệu ghép nhóm a) Bảng tần số ghép nhóm
1. Mẫu số liệu ghép nhóm
a) Bảng tần số ghép nhóm
- Mẫu số liệu ghép nhóm là mẫu số liệu cho dưới dạng bảng tần số ghép nhóm.
- Mỗi nhóm số liệu gồm một số giá trị của mẫu số liệu được ghép nhóm theo một tiêu chí xác định có dạng [a; b), trong đó a là đầu mút trái, b là đầu mút phải. Độ dài nhóm là b – a.
- Tần số của một nhóm là số số liệu trong mẫu số liệu thuộc vào nhóm đó. Tần số của nhóm 1, nhóm 2, …, nhóm m kí hiệu lần lượt là n1, n2, …, nm.
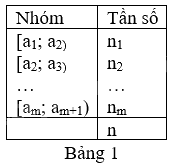
- Bảng tần số ghép nhóm được lập như ở bảng 1, trong đó mẫu liệu gồm n số liệu được chia thành m nhóm ứng với m nửa khoảng [a1; a2); [a2; a3); …;[am; am+1), ở đó
a1 < a2 < … < am < am+1 và n = n1 + n2 + … + nm.
b) Ghép nhóm mẫu số liệu. Tần số tích lũy
Để chuyển mẫu số liệu không ghép nhóm thành mẫu số liệu ghép nhóm, ta thực hiện như sau:
- Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước;
- Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng tần số ghép nhóm.
Chú ý: Khi ghép nhóm số liệu, ta thường phân chia các nhóm có độ dài bằng nhau và đầu mút của các nhóm có thể không phải là giá trị của mẫu số liệu. Nhóm cuối cùng có thể là [am; am+1].
- Tần số tích lũy của một nhóm là số số liệu trong mẫu số liệu có giá trị nhỏ hơn giá trị đầu mút phải của nhóm đó. Tần số tích lũy của nhóm 1, nhóm 2, …, nhóm m kí hiệu lần lượt là \(c{f_1},c{f_2},...,c{f_m}\).
- Bảng tần số ghép nhóm bao gồm cả tần số tích lũy được lập như ở Bảng 2.

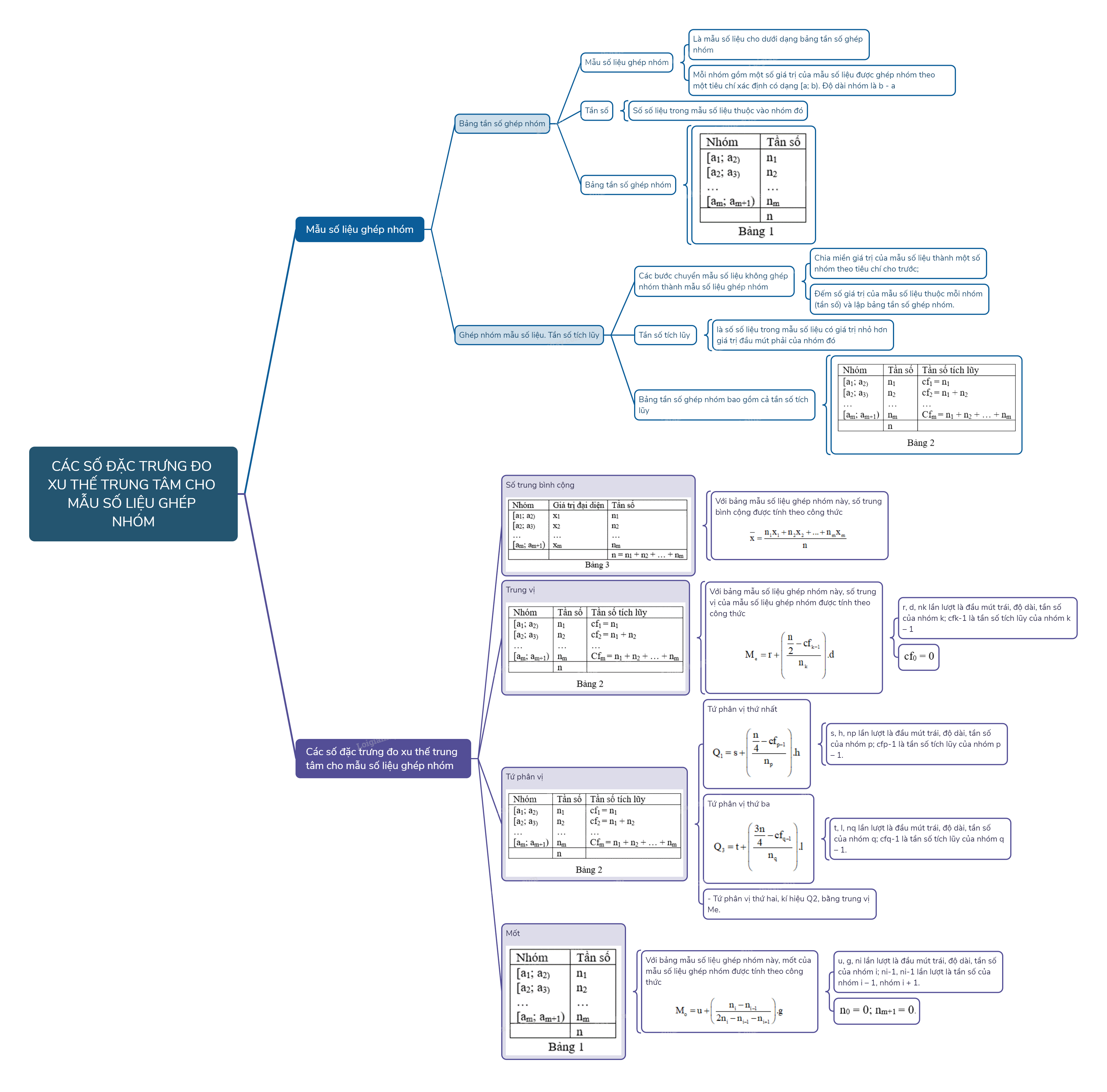
2. Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm
a) Số trung bình cộng
Cho mẫu số liệu ghép nhóm như ở bảng 3, trong đó giá trị đại diện của nhóm là trung điểm xi của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm i.

Số trung bình cộng của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính theo công thức
\(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_m}{x_m}}}{n}\)
b) Trung vị
Cho mẫu số liệu ghép nhóm bao gồm cả tần số tích lũy như ở Bảng 2.
Giả sử nhóm k là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{2}\), tức là \(c{f_{k - 1}} < \frac{n}{2}\) nhưng \(c{f_k} \ge \frac{n}{2}\). Ta gọi r, d, nk lần lượt là đầu mút trái, độ dài, tần số của nhóm k; cfk-1 là tần số tích lũy của nhóm k – 1.
Trung vị của mẫu số liệu ghép nhóm, kí hiệu Me, được tính theo công thức sau:
\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d\)
Quy ước: cf0 = 0.
c) Tứ phân vị
Cho mẫu số liệu ghép nhóm bao gồm cả tần số tích lũy như ở Bảng 2.
- Tứ phân vị thứ hai, kí hiệu Q2, bằng trung vị Me.
- Giả sử nhóm p là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{4}\), tức là \(c{f_{p - 1}} < \frac{n}{4}\) nhưng \(c{f_p} \ge \frac{n}{4}\). Ta gọi s, h, np lần lượt là đầu mút trái, độ dài, tần số của nhóm p; cfp-1 là tần số tích lũy của nhóm p – 1.
Tứ phân vị thứ nhất, kí hiệu Q1, được tính bằng công thức sau:
\({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h\)
- Giả sử nhóm q là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{3n}}{4}\), tức là \(c{f_{q - 1}} < \frac{{3n}}{4}\) nhưng \(c{f_q} \ge \frac{{3n}}{4}\). Ta gọi t, l, nq lần lượt là đầu mút trái, độ dài, tần số của nhóm q; cfq-1 là tần số tích lũy của nhóm q – 1.
Tứ phân vị thứ ba, kí hiệu Q3, được tính bằng công thức sau:
\({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l\)
d) Mốt
Cho mẫu số liệu ghép nhóm như ở Bảng 1.
Giả sử nhóm i là nhóm có tần số lớn nhất. Ta gọi u, g, ni lần lượt là đầu mút trái, độ dài, tần số của nhóm i; ni-1, ni-1 lần lượt là tần số của nhóm i – 1, nhóm i + 1.
Mốt của mẫu số liệu ghép nhóm, kí hiệu Mo, được tính theo công thức sau:
\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g\)
Quy ước: n0 = 0; nm+1 = 0.
Trong thống kê, các số đặc trưng đo xu thế trung tâm đóng vai trò quan trọng trong việc tóm tắt và mô tả một tập dữ liệu. Chúng giúp chúng ta hiểu được giá trị điển hình hoặc trung tâm của dữ liệu. Đối với mẫu số liệu ghép nhóm, việc tính toán các số đặc trưng này có một số điểm khác biệt so với mẫu số liệu không ghép nhóm.
Mẫu số liệu ghép nhóm là tập hợp các dữ liệu được chia thành các khoảng hoặc lớp. Mỗi lớp được xác định bởi một khoảng giá trị và tần số tương ứng, cho biết số lượng dữ liệu thuộc về khoảng đó. Ví dụ, một bảng tần số có thể biểu diễn số lượng học sinh đạt điểm trong các khoảng điểm khác nhau.
Trung bình cộng (x̄) của mẫu số liệu ghép nhóm được tính theo công thức:
x̄ = (∑(xi * fi)) / n
Trong đó:
Trung điểm của một khoảng được tính bằng (giới hạn dưới + giới hạn trên) / 2.
Trung vị (M) là giá trị nằm ở giữa tập dữ liệu khi được sắp xếp theo thứ tự tăng dần. Để tìm trung vị của mẫu số liệu ghép nhóm, ta thực hiện các bước sau:
M = xm + ((n/2 - Fm-1) / fm) * h
Trong đó:
Mốt (Mo) là giá trị xuất hiện nhiều nhất trong tập dữ liệu. Đối với mẫu số liệu ghép nhóm, ta tìm khoảng chứa mốt, tức là khoảng có tần số lớn nhất. Nếu có nhiều khoảng có tần số lớn nhất, ta có thể nói rằng dữ liệu có nhiều mốt.
Mốt có thể được ước tính bằng cách sử dụng công thức:
Mo = xm + ((fm - fm-1) / ((fm - fm-1) + (fm - fm+1))) * h
Trong đó:
Giả sử ta có bảng tần số sau:
| Khoảng | Tần số (fi) |
|---|---|
| [0-10) | 5 |
| [10-20) | 10 |
| [20-30) | 15 |
| [30-40) | 8 |
| [40-50) | 2 |
Tổng số tần số n = 5 + 10 + 15 + 8 + 2 = 40
Trung điểm của các khoảng lần lượt là 5, 15, 25, 35, 45.
Trung bình cộng: x̄ = ((5*5) + (15*10) + (25*15) + (35*8) + (45*2)) / 40 = 26.25
Trung vị: n/2 = 20. Khoảng chứa trung vị là [20-30) vì tần số tích lũy của [0-20) là 15 và tần số tích lũy của [20-30) là 30. M = 25 + ((20 - 15) / 15) * 10 = 28.33
Mốt: Khoảng [20-30) có tần số lớn nhất là 15. xm = 25, fm = 15, fm-1 = 10, fm+1 = 8, h = 10. Mo = 25 + ((15 - 10) / ((15 - 10) + (15 - 8))) * 10 = 26.67
Các số đặc trưng đo xu thế trung tâm được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Việc hiểu rõ về các số đặc trưng này giúp chúng ta đưa ra những quyết định chính xác và hiệu quả hơn dựa trên dữ liệu.