Giải Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều: Giải tích chi tiết

Bài 14 trang 56 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc giải các bài toán liên quan đến đạo hàm của hàm số. Bài học này giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng vào giải quyết các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 14 trang 56, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

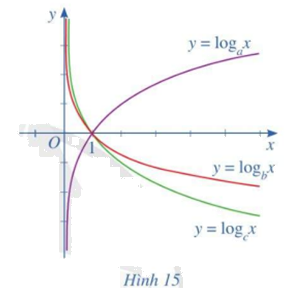
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit (y = {log _a}x;,y = {log _b}x;,y = {log _c}x) được cho bởi Hình 15.

Đề bài

Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều 1

A. c < a < b

B. c < b < a

C. a < b < c

D. b < c < a

Phương pháp giải - Xem chi tiết Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều 2

Dựa vào các hệ số và tính đồng biến, nghịch biến của hàm số lôgarit để suy ra

Lời giải chi tiết

- Do \(y = {\log _a}x\) đồng biến => a lớn nhất => Loại A, C

- Do \({\log _b}x > {\log _c}x\) theo đồ thị. Mà \(y = {\log _b}x;\,y = {\log _c}x\) nghịch biến nê b < c => Chọn D

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều – hành trang không thể thiếu trong chuyên mục toán 11 trên nền tảng toán học. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về các quy tắc tính đạo hàm, đặc biệt là quy tắc tính đạo hàm của tổng, hiệu, tích, thương và đạo hàm hàm hợp để giải quyết các bài toán cụ thể.

Nội dung bài tập Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều

Bài 14 thường bao gồm các dạng bài tập sau:

Tính đạo hàm của hàm số tại một điểm cho trước.
Tìm đạo hàm của hàm số.
Xác định hệ số góc của tiếp tuyến của đồ thị hàm số tại một điểm.
Ứng dụng đạo hàm để giải các bài toán liên quan đến tốc độ thay đổi.

Hướng dẫn giải Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều

Để giải Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều một cách hiệu quả, học sinh cần:

Nắm vững các quy tắc tính đạo hàm cơ bản.
Phân tích cấu trúc của hàm số để lựa chọn phương pháp tính đạo hàm phù hợp.
Thực hành giải nhiều bài tập tương tự để rèn luyện kỹ năng.

Ví dụ minh họa giải Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều

Ví dụ 1: Tính đạo hàm của hàm số f(x) = x³ + 2x² - 5x + 1.

Giải:

f'(x) = 3x² + 4x - 5

Ví dụ 2: Tìm đạo hàm của hàm số g(x) = sin(x) * cos(x).

Giải:

g'(x) = cos(x) * cos(x) + sin(x) * (-sin(x)) = cos²(x) - sin²(x)

Các lưu ý khi giải Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều

Chú ý đến các quy tắc tính đạo hàm của hàm hợp.
Kiểm tra lại kết quả sau khi tính đạo hàm.
Sử dụng máy tính cầm tay để kiểm tra kết quả.

Tầm quan trọng của việc nắm vững kiến thức về đạo hàm

Kiến thức về đạo hàm là nền tảng quan trọng cho việc học các chương trình Toán học nâng cao, đặc biệt là giải tích. Đạo hàm được ứng dụng rộng rãi trong nhiều lĩnh vực khoa học kỹ thuật, kinh tế, và đời sống.

Bài tập luyện tập thêm về đạo hàm

Để củng cố kiến thức về đạo hàm, học sinh có thể tham khảo thêm các bài tập sau:

Tính đạo hàm của các hàm số sau: h(x) = e^x, k(x) = ln(x), l(x) = tan(x).
Tìm đạo hàm bậc hai của hàm số f(x) = x⁴ - 3x² + 2.
Giải các bài toán ứng dụng đạo hàm để tìm cực trị của hàm số.

Kết luận

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Việc nắm vững các quy tắc tính đạo hàm và thực hành giải nhiều bài tập sẽ giúp học sinh tự tin hơn trong việc giải quyết các bài toán liên quan đến đạo hàm.