Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 108, 109 SGK Toán 11 tập 1 - Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, đặc biệt là trong môn Toán.
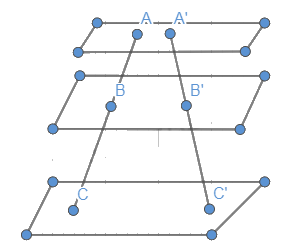
Cho ba mặt phẳng song song (P), (Q), (R). Hai cát tuyến bất kì a và a’ cắt ba mặt phẳng song song lần lượt tại các điểm A, B, C và A’, B’, C’. Gọi \({B_1}\) là giao điểm của AC’ với mặt phẳng (Q) (Hình 66).
Cho ba mặt phẳng song song (P), (Q), (R). Hai cát tuyến bất kì a và a’ cắt ba mặt phẳng song song lần lượt tại các điểm A, B, C và A’, B’, C’. Gọi \({B_1}\) là giao điểm của AC’ với mặt phẳng (Q) (Hình 66).
a) Nêu vị trí tương đối của \(B{B_1}\) và \(CC'\);\({B_1}B\) và \(AA'\)
b) Có nhận xét gì về các tỉ số:
\(\frac{{AB}}{{A{B_1}}}, \frac{{BC}}{{{B_1}C'}}\) và \(\frac{{CA}}{{C'A'}}; \frac{{A{B_1}}}{{A'B'}},\frac{{{B_1}C'}}{{B'C'}}\) và \(\frac{{C'A}}{{C'A'}}\)
c) Từ kết quả câu a) và câu b:, so sánh các tỉ số:
\(\frac{{AB}}{{A'B'}},\frac{{BC}}{{B'C'}}\)và\(\frac{{CA}}{{C'A'}}\)
Phương pháp giải:
Định lý Ta-let:
Nếu a, b là hai cát tuyến bất kỳ cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)
Lời giải chi tiết:
a) \(B{B_1}\)và\(CC'\)song song với nhau
\({B_1}B\)và\(AA'\)song song với nhau
b) Các tỉ số:
\(\frac{{AB}}{{A{B_1}}} = \frac{{BC}}{{{B_1}C'}} = \frac{{CA}}{{C'A'}}\)
\(\frac{{A{B_1}}}{{A'B'}} = \frac{{{B_1}C'}}{{B'C'}} = \frac{{C'A}}{{C'A'}}\)
c) Các tỉ số:\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)
Bạn Minh cho rằng: Nếu a, b là cát tuyến bất kì cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} = \frac{{AC}}{{A'C'}}\)
Phát biểu của bạn Minh có đúng không? Vì sao?

Phương pháp giải:
Nếu a,b là hai cát tuyến bất kì cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A,B, C và A’, B’, C’ thì
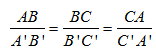
Lời giải chi tiết:
Bạn Minh phát biểu sai vì \(\frac{{CA}}{{C'A'}} = \frac{{AB + BC}}{{A'B' + B'C'}} \ne \frac{{AB}}{{BC}} \ne \frac{{A'B'}}{{B'C'}}\)
Mục 3 trong SGK Toán 11 tập 1 - Cánh Diều tập trung vào việc nghiên cứu về phép biến hình affine. Đây là một phần quan trọng trong chương trình học, giúp học sinh hiểu rõ hơn về các phép biến hình trong mặt phẳng và ứng dụng của chúng trong giải quyết các bài toán hình học.
Mục 3 bao gồm các nội dung chính sau:
Dưới đây là lời giải chi tiết cho các bài tập trong mục 3 trang 108, 109 SGK Toán 11 tập 1 - Cánh Diều:
Để tìm ma trận của phép biến hình affine f, ta cần xác định ma trận A sao cho:
[x'] = [a b] [x] [y'] [c d] [y]
Trong trường hợp này, x' = x + 2y và y' = 3x - y. Do đó, ta có:
a = 1, b = 2, c = 3, d = -1
Vậy ma trận của phép biến hình affine f là:
[1 2] [3 -1]
Để tìm ảnh của tam giác ABC qua phép biến hình affine f, ta cần tính ảnh của từng đỉnh A, B, C:
Vậy ảnh của tam giác ABC qua phép biến hình affine f là tam giác A'B'C' với A'(3; 0), B'(7; 2), C'(6; 9).
Để chứng minh rằng phép biến hình affine f bảo toàn diện tích, ta cần chứng minh rằng diện tích của hình biến hình bằng diện tích của hình gốc. Gọi S là diện tích của hình gốc và S' là diện tích của hình biến hình. Ta có:
S' = |det(A)| * S
Trong đó, A là ma trận của phép biến hình affine f:
[a b] [d e]
det(A) = ae - bd
Nếu det(A) = 1 thì S' = S, tức là phép biến hình affine f bảo toàn diện tích.
Để nắm vững kiến thức về phép biến hình affine, các em nên:
Hy vọng rằng lời giải chi tiết bài tập mục 3 trang 108, 109 SGK Toán 11 tập 1 - Cánh Diều sẽ giúp các em hiểu rõ hơn về phép biến hình affine và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!