Bài 7 trang 56 SGK Toán 11 tập 1 thuộc chương trình Giải tích, tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tính toán và tư duy logic.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự. Chúng tôi luôn cập nhật nội dung mới nhất, đảm bảo tính chính xác và phù hợp với chương trình học.
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thể cao xuống với dây đai an toàn buộc xung quanh người)
Đề bài
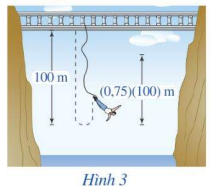
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100m. Giả sử sau mỗi lần rơi xuống, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần rơi xuống và lại được kéo lên, tính từ lúc bắt đầu nhảy (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải - Xem chi tiết
Dựa vào công thức cấp số nhân để xác định.
Lời giải chi tiết
Gọi \({u_n}\) là quãng đường người đó rơi xuống lần thứ n.
Khi đó:
\({u_1} = 100\);
\({u_2} = 100.(75\% ) = 75\);
\({u_3} = 100.{(75\% )^2} = 56,25\);
…
Dãy số này lập thành một cấp số nhân có số hạng đầu là 100 và công bội q = 75%, có công thức tổng quát \(u_n = 100.(75\%)^{n-1}\) (m).
Tổng quãng đường người đó đi được khi rơi xuống 10 lần là:
\({S_{10}} = 100.\frac{{1 - {{\left( {75\% } \right)}^n}}}{{1 - 75\% }} \approx 377,47\) (m).
Nhận xét: Người đó sau khi rơi xuống lần 1 thì được kéo lên độ cao bằng quãng đường khi rơi xuống lần 2.
Gọi \({v_n}\) là quãng đường người đó được kéo lên lần thứ n.
Khi đó: \({v_1} = {u_2}\); \({v_2} = {u_3}\);…; \({v_{10}} = {u_{11}}\).
Tổng quãng đường người đó được kéo lên sau 10 lần rơi là:
\(S{'_{10}} = {v_1} + ... + {v_{10}} = {u_2} + ... + {u_{11}}\)
\( = {S_{11}} - {u_1} = 100\frac{{1 - {{(75\% )}^{11}}}}{{1 - 75\% }} - 100 \approx 283,11\) (m).
Vậy tổng quãng đường người đó đi được tính cả rơi xuống và được kéo lên sau 10 lần rơi là khoảng 660 mét.
Bài 7 trang 56 SGK Toán 11 tập 1 - Cánh diều yêu cầu học sinh giải các bài toán liên quan đến đạo hàm của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp.
Trước khi đi vào giải bài tập cụ thể, chúng ta cần ôn tập lại một số kiến thức lý thuyết quan trọng:
Để minh họa, chúng ta sẽ xem xét một ví dụ cụ thể từ bài 7 trang 56 SGK Toán 11 tập 1 - Cánh diều. Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = 2x3 + 5x2 - 3x + 1.
Để củng cố kiến thức, học sinh nên tự giải thêm các bài tập tương tự. Dưới đây là một số bài tập luyện tập:
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác. Một số ứng dụng quan trọng bao gồm:
Khi giải bài tập về đạo hàm, học sinh cần lưu ý một số điều sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải Bài 7 trang 56 SGK Toán 11 tập 1 - Cánh diều và các bài tập tương tự. Chúc các em học tốt!