Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 3, 4, 5 sách giáo khoa Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Có 13 ô tô có độ tuổi dưới 4;
Trong bảng 1 ở phần mở đầu, ta thấy:
Có 13 ô tô có độ tuổi dưới 4;
Có 29 ô tô có độ tuổi dưới 8.
Hãy xác định số ô tô có độ tuổi:
a) Từ 8 đến dưới 12
b) Từ 12 đến dưới 16
c) Từ 16 đến dưới 20
Phương pháp giải:
Nhìn vào cột tần số để xác định số ô tô từng độ tuổi
Lời giải chi tiết:
a) Số ô tô có độ tuổi từ 8 đến dưới 12 là 48 ô tô
b) Số ô tô có độ tuổi từ 12 đến 16 là 22 ô tô
c) Số ô tô có độ tuổi từ 16 đến 20 là 8 ô tô
Mẫu số liệu ghép nhóm ở Bảng 1 có bao nhiêu số liệu? Bao nhiêu nhóm? Tìm tần số của mỗi nhóm?

Phương pháp giải:
Dựa vào công thức đã cho để xác định
Lời giải chi tiết:
- Mẫu số liệu ghép nhóm ở Bảng 1 có 120 số liệu
- Có 5 nhóm
- Tần số của mỗi nhóm:
Một trường trung học phổ thông chọn 36 học sinh nam của khối lớp 11, đo chiều cao của các bạn học sinh đó và thu được mẫu số liệu sau (đơn vị: centimet):

Từ mẫu số liệu không ghép nhóm trên, hãy ghép các số liệu thành năm nhóm theo các nửa khoảng có độ dài bằng nhau.
Phương pháp giải:
Để chuyển mẫu số liệu không ghép nhóm thành mẫu số liệu ghép nhóm, ta thực hiện như sau:
- Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước
- Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng tần số ghép nhóm
Lời giải chi tiết:
- Ta chia bảng ghép nhóm thành các phần có độ dài bằng nhau: [160; 163); [163; 166); [166; 169); [169; 172); [172; 175)
Một thư viện thống kê số người đến đọc sách vào buổi trong 30 ngày của tháng vừa qua như sau:

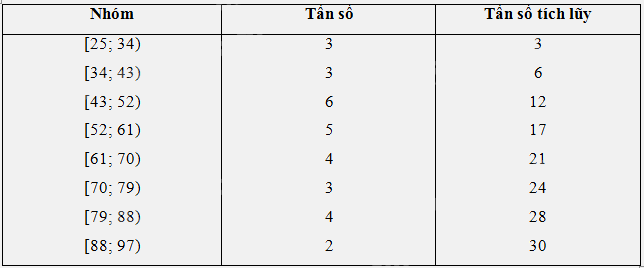
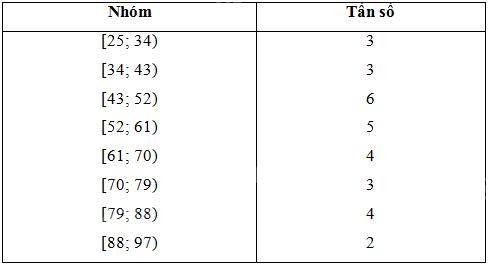
Lập bảng tần số ghép nhóm có tám nhóm ứng với tám nửa khoảng sau: [25; 34); [34; 43); [43; 52); [52; 61); [61; 70); [70; 79); [79; 88); [88; 97)
Phương pháp giải:
Dựa vào những kiến thức vừa học để làm bài
Lời giải chi tiết:

Trong Bảng 4 , có bao nhiêu số liệu với giá trị không vượt quá giá trị của đầu mút phải

a) 163 của nhóm 1
b) 166 của nhóm 2
c) 169 của nhóm 3
d) 172 của nhóm 4
e) 175 của nhóm 5
Phương pháp giải:
Lấy tần số của từng phần cộng lại với nhau
Lời giải chi tiết:
Các giá trị không vượt quá giá trị của đầu mút phải:
a) 163 của nhóm 1: 6
b) 166 của nhóm 2: 18
c) 169 của nhóm 3: 28
d) 172 của nhóm 4: 33
e) 175 của nhóm 5: 36
Trong bài toán ở Luyện tập 2, lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có tám nhóm ứng với tám nửa khoảng: [25; 34); [34; 43); [43; 52); [52; 61); [61; 70); [70; 79);
[79; 88); [88; 97)
Phương pháp giải:
Dựa vào kiến thức tần số tích lũy vừa học để xác định
Lời giải chi tiết:

Mục 1 của SGK Toán 11 tập 2 - Cánh Diều tập trung vào việc ôn tập chương trình Đại số và Giải tích ở lớp 10, đồng thời giới thiệu một số kiến thức cơ bản về hàm số và đồ thị hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài 1 yêu cầu xác định tập xác định của hàm số. Để giải bài này, cần nhớ lại điều kiện xác định của các hàm số cơ bản như phân thức, căn bậc hai, logarit. Ví dụ, với hàm số y = 1/(x-2), tập xác định là R \ {2}.
Bài 2 thường liên quan đến việc xét tính chẵn lẻ của hàm số. Một hàm số được gọi là chẵn nếu f(-x) = f(x) với mọi x thuộc tập xác định. Hàm số được gọi là lẻ nếu f(-x) = -f(x) với mọi x thuộc tập xác định.
Bài 3 có thể yêu cầu vẽ đồ thị hàm số hoặc tìm điểm thuộc đồ thị. Để vẽ đồ thị, cần xác định các điểm đặc biệt như giao điểm với trục tọa độ, điểm cực trị, điểm uốn. Sử dụng các phép biến hình đồ thị có thể giúp vẽ nhanh và chính xác hơn.
Ví dụ: Giải phương trình 2x2 - 5x + 2 = 0.
Lời giải:
Δ = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9 > 0
x1 = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
x2 = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 1/2
Vậy phương trình có hai nghiệm phân biệt x1 = 2 và x2 = 1/2.
Khi giải các bài tập về hàm số, cần chú ý đến tập xác định của hàm số. Ngoài ra, việc vẽ đồ thị hàm số giúp hiểu rõ hơn về tính chất của hàm số và tìm ra lời giải chính xác.
Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 3, 4, 5 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt!