Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 51, 52, 53 sách giáo khoa Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ (y = {left( {frac{1}{2}} right)^x}).
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, hãy tìm x sao cho \({\left( {\frac{1}{2}} \right)^x} > 2\)
Phương pháp giải:
Dựa vào nhìn đồ thị để xét tính đồng biến nghịch biến
Lời giải chi tiết:
- Hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên toàn R
- Dựa vào đồ thị ta thấy: \({\left( {\frac{1}{2}} \right)^x} > 2 \Leftrightarrow x > - 1\)
Cho hai ví dụ về bất phương trình mũ cơ bản
Phương pháp giải:
Dựa vào định nghĩa bất phương trình mũ để xác định
Lời giải chi tiết:
Ví dụ:
+ \({3^x} = 9\)
+ \({4^{x + 2}} = 16\)
Giải mỗi bất phương trình sau:
a) \({7^{x + 3}} < 343\)
b) \({\left( {\frac{1}{4}} \right)^x} \ge 3\)
Phương pháp giải:
Dựa vào ví dụ 10 để làm
Lời giải chi tiết:
a) \({7^{x + 3}} < 343\)
\(\begin{array}{l} \Leftrightarrow x + 3 < {\log _7}343\\ \Leftrightarrow x + 3 < 3\\ \Leftrightarrow x < 0\end{array}\)
Vậy tập nghiệm của bất phương trình là: \(\left( { - \infty ;0} \right)\)
b) \({\left( {\frac{1}{4}} \right)^x} \ge 3\)
\( \Leftrightarrow x \le {\log _{\frac{1}{4}}}3\)
Vậy tập nghiệm của bất phương trình là: \(\left( { - \infty ;{{\log }_{\frac{1}{4}}}3} \right]\)
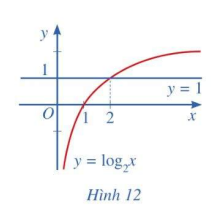
Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit \(y = {\log _2}x\). Từ đó, hãy tìm x sao cho \({\log _2}x > 1\)

Phương pháp giải:
Dựa vào nhìn đồ thị để xét tính đồng biến nghịch biến
Lời giải chi tiết:
- Hàm số \(y = {\log _2}x\) đồng biến trên tập xác định
- Dựa vào đồ thị ta thấy: \({\log _2}x > 1 \Leftrightarrow x > 2\)
Cho hai ví dụ về bất phương trình logarit cơ bản
Phương pháp giải:
Dựa vào định nghĩa để làm
Lời giải chi tiết:
Giải mỗi bất phương trình sau:
a) \({\log _3}x < 2\)
b) \({\log _{\frac{1}{4}}}\left( {x - 5} \right) \ge - 2\)
Phương pháp giải:
Dựa vào ví dụ 13 để làm
Lời giải chi tiết:
a) \({\log _3}x < 2\)
\(\begin{array}{l} \Leftrightarrow 0 < x < {3^2}\\ \Leftrightarrow 0 < x < 9\end{array}\)
Vậy tập nghiệm của bất phương trình là (0 ; 9)
b) \({\log _{\frac{1}{4}}}\left( {x - 5} \right) \ge - 2\)
\(\begin{array}{l} \Leftrightarrow 0 < x - 5 \le {\left( {\frac{1}{4}} \right)^{ - 2}}\\ \Leftrightarrow 5 < x \le 21\end{array}\)
Vậy tập nghiệm của bất phương trình là \(\left( {5;21} \right]\)
Mục 2 của chương trình Toán 11 tập 2 - Cánh Diều tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng, đặt nền móng cho các kiến thức hình học không gian phức tạp hơn ở các lớp trên. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập trong mục này là rất cần thiết.
Bài tập này yêu cầu học sinh vận dụng các định lý về quan hệ song song giữa đường thẳng và mặt phẳng, giữa hai mặt phẳng để chứng minh các tính chất hình học. Các em cần nắm vững các dấu hiệu nhận biết đường thẳng song song với mặt phẳng, mặt phẳng song song với mặt phẳng.
Bài tập này tập trung vào các kiến thức về đường thẳng vuông góc với mặt phẳng, hai mặt phẳng vuông góc. Học sinh cần hiểu rõ các định nghĩa, tính chất và dấu hiệu nhận biết các quan hệ vuông góc này.
Bài tập này liên quan đến việc tính khoảng cách từ một điểm đến mặt phẳng, từ một điểm đến đường thẳng, giữa hai đường thẳng chéo nhau. Các em cần nắm vững công thức tính khoảng cách và các phương pháp giải bài toán liên quan.
| Công thức | Mô tả |
|---|---|
| d(M, (P)) | Khoảng cách từ điểm M đến mặt phẳng (P) |
| d(M, d) | Khoảng cách từ điểm M đến đường thẳng d |
Để giải các bài tập trong mục 2 này một cách hiệu quả, các em nên:
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu, kèm theo các chú thích và giải thích cần thiết.
(Lời giải chi tiết cho từng bài tập sẽ được trình bày ở đây, bao gồm các bước giải, công thức sử dụng, và kết luận.)
Hy vọng với những kiến thức và lời giải chi tiết trên, các em học sinh đã nắm vững được các nội dung quan trọng trong mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!