Chào mừng bạn đến với bài học về lý thuyết các phép biến đổi lượng giác trong chương trình Toán 11 Cánh Diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và các công thức quan trọng để giải quyết các bài toán liên quan đến lượng giác.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học tập trực tuyến hiệu quả và thú vị. Hãy cùng bắt đầu khám phá thế giới lượng giác ngay bây giờ!
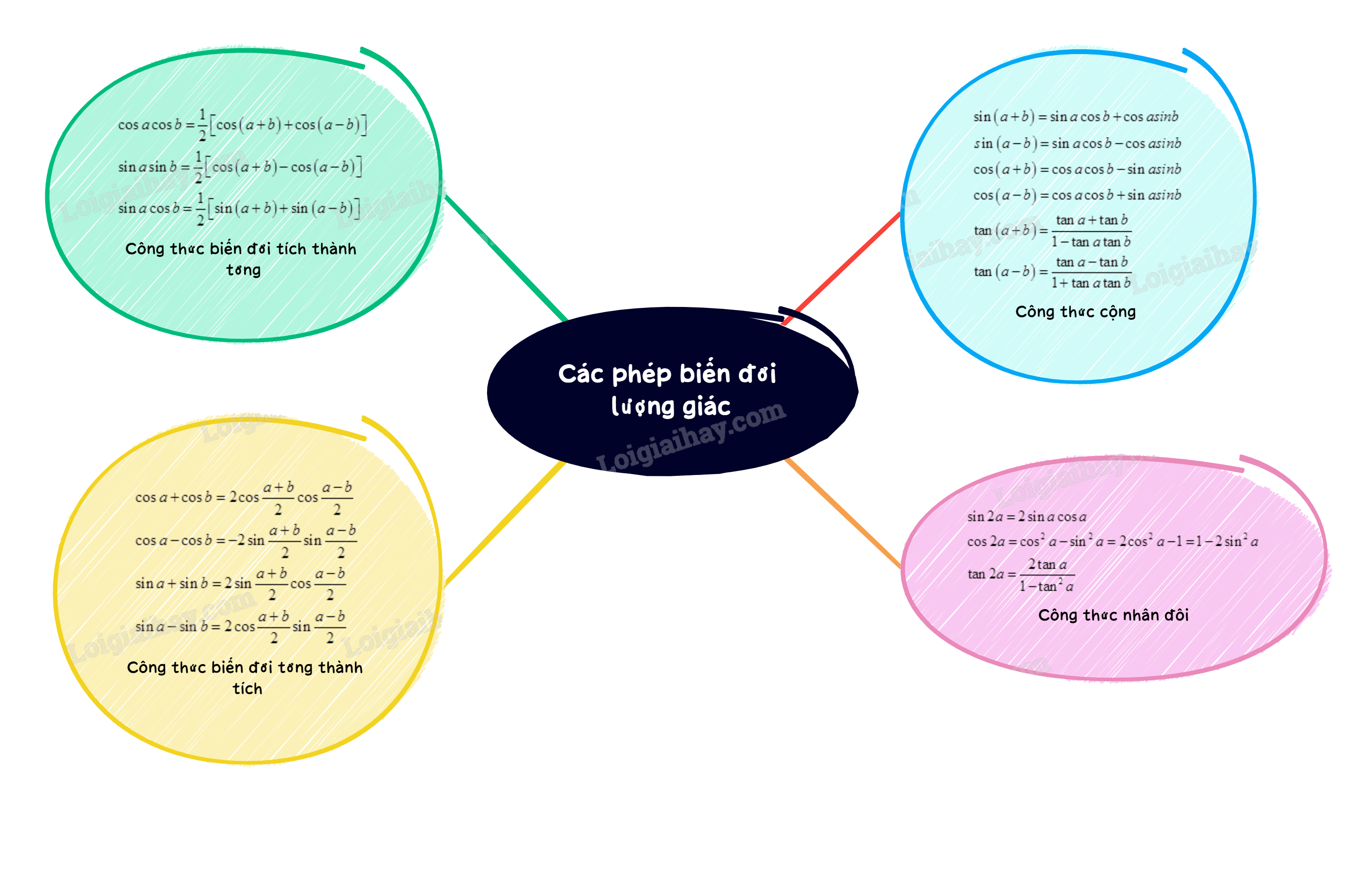
I. Công thức cộng
I. Công thức cộng
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a - b} \right) = \sin a\cos b - \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b - \sin asinb\\\cos \left( {a - b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\\\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\end{array}\)
II. Công thức nhân đôi
\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\end{array}\)
Suy ra, công thức hạ bậc:
\({\sin ^2}a = \frac{{1 - \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)
III. Công thức biến đổi tích thành tổng
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}\)
IV. Công thức biến đổi tổng thành tích
\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\end{array}\)
Chương trình Toán 11 Cánh Diều, phần lượng giác, đặc biệt chú trọng đến các phép biến đổi lượng giác. Việc nắm vững lý thuyết này là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình và các kỳ thi quan trọng.
Trước khi đi sâu vào các phép biến đổi, chúng ta cần ôn lại các công thức lượng giác cơ bản:
Có nhiều phép biến đổi lượng giác khác nhau, nhưng phổ biến nhất là:
Các phép biến đổi lượng giác có rất nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Ví dụ 1: Tính sin(75o)
Ta có: sin(75o) = sin(45o + 30o) = sin(45o)cos(30o) + cos(45o)sin(30o) = (√2/2)(√3/2) + (√2/2)(1/2) = (√6 + √2) / 4
Ví dụ 2: Chứng minh đẳng thức: cos2(x) - sin2(x) = cos(2x)
Ta có: cos(2x) = cos2(x) - sin2(x) (đây là công thức nhân đôi đã được học)
Để nắm vững lý thuyết và kỹ năng giải bài tập về các phép biến đổi lượng giác, bạn nên:
Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!