Góc lượng giác là một khái niệm quan trọng trong chương trình Toán 11, đặc biệt là với sách Cánh Diều. Nắm vững lý thuyết về góc lượng giác và giá trị lượng giác là bước đệm quan trọng để giải quyết các bài toán hình học và lượng giác phức tạp hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu về chủ đề này, giúp bạn tự tin chinh phục môn Toán.
I. Góc lượng giác
I. Góc lượng giác
1. Góc hình học và số đo của chúng
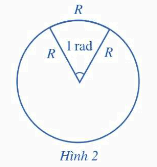
*Nhận xét:
- Đơn vị đo góc: độ hoặc radian (rad).
- Ta có: \({180^o} = \pi \)rad, do đó 1 rad \( = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \left( {\frac{\pi }{{180}}} \right)\)rad.
- Người ta thường không viết chữ radian hay rad sau số đo góc.
VD: \(\frac{\pi }{2}\)rad cũng được viết là \(\frac{\pi }{2}\).
2. Góc lượng giác và số đo của chúng
a, Khái niệm
- Cho 2 tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
- Mỗi góc lượng giác được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.
b, Tính chất
- Cho hai góc lượng giác = và (O’u’,O’v’) có tia đầu trùng nhau \(\left( {Ou \equiv O'u'} \right)\), tia cuối trùng nhau \(\left( {Ov \equiv O'v'} \right)\).
Khi đó, nếu sử dụng đợn vị đo là độ thì ta có:
\(\left( {Ou,Ov} \right) = \left( {O'u',O'v'} \right) + k{360^o},k \in \mathbb{Z}.\)
Nếu sử dụng đơn vị đo là radian thì:
\(\left( {Ou,Ov} \right) = \left( {O'u',O'v'} \right) + k2\pi ,k \in \mathbb{Z}.\)
* Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
(Ou,Ov) + (Ov, Ow) = (Ou,Ow) \( + k2\pi ,k \in \mathbb{Z}.\)
II. Giá trị lượng giác của góc lượng giác
1. Đường tròn lượng giác
Trong mặt phẳng toa độ đã được định hướng Oxy, lấy điểm A(1;0). Đường tròn tâm O, bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.
2. Giá trị lượng giác của góc lượng giác
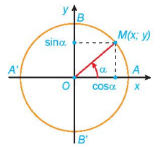
- Trục tung là trục sin, trục hoành là trục côsin.
- Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\)
* Dấu của các giá trị lượng giác của góc \(\alpha \)
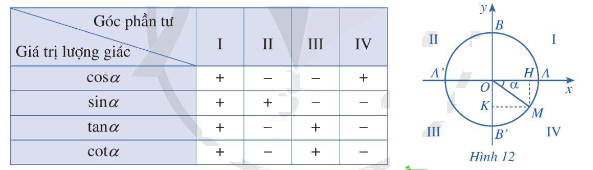
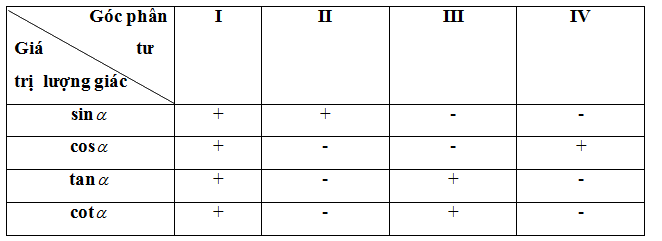
* Các công thức lượng giác cơ bản
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
3. Giá trị lượng giác của các góc có liên quan đặc biệt
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)
4. Sử dụng máy tính cầm tay để tính giá trị của một góc lượng giác
Đơn vị độ:

Đơn vị radian:

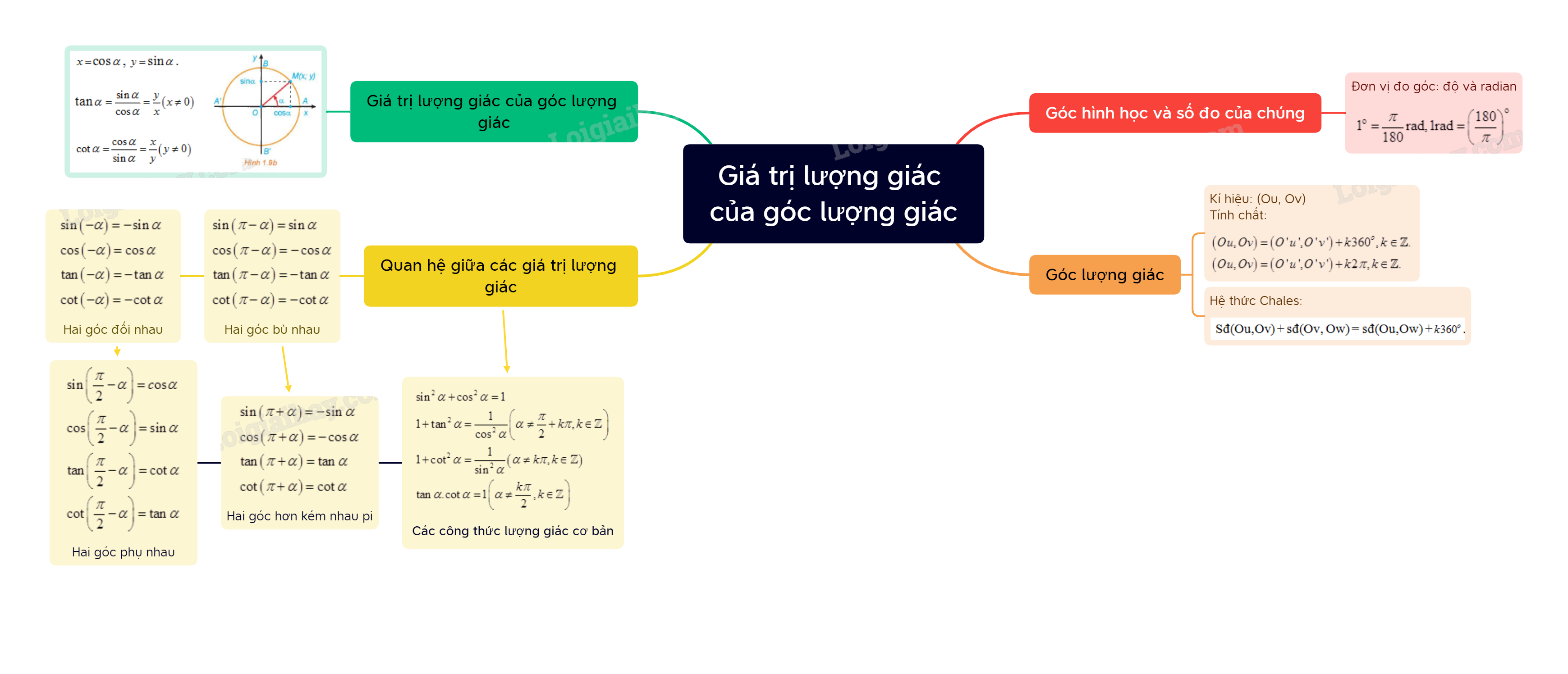
Góc lượng giác là một khái niệm mở rộng của góc hình học, cho phép đo các góc lớn hơn 360 độ. Để hiểu rõ về góc lượng giác, chúng ta cần nắm vững các khái niệm cơ bản sau:
Trên đường tròn lượng giác, một góc lượng giác α được xác định bởi một tia Om quay từ tia Ox theo chiều dương. Số đo của góc α bằng số đo của cung am trên đường tròn lượng giác.
| Góc α | sin α | cos α | tan α | cot α |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | Không xác định |
| 30° | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | 1 | 0 | Không xác định | 0 |
Các công thức này giúp chúng ta tính toán giá trị lượng giác của các góc mà không cần sử dụng máy tính:
Để tính giá trị lượng giác của các góc lớn hơn 360°, ta có thể sử dụng tính chất chu kỳ của hàm lượng giác. Ví dụ, sin(360° + α) = sin α.
Lý thuyết góc lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Để củng cố kiến thức về lý thuyết góc lượng giác, bạn có thể thực hành giải các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với tài liệu này, bạn sẽ nắm vững lý thuyết góc lượng giác và tự tin giải quyết các bài toán liên quan. Chúc bạn học tập tốt!