Chào mừng bạn đến với bài giải Bài 2 trang 94 SGK Toán 11 tập 2 - Cánh diều trên giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ bạn học toán hiệu quả và đạt kết quả tốt nhất.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, hai đường thẳng \(AC\) và \(BD\) cắt nhau tại \(O\)
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, hai đường thẳng \(AC\) và \(BD\) cắt nhau tại \(O\), \(SO \bot \left( {ABCD} \right)\), tam giác \(SAC\) là tam giác đều.
a) Tính số đo của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\).
b) Chứng minh rằng \(AC \bot \left( {SBD} \right)\). Tính số đo của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\).
c) Gọi \(M\) là trung điểm của cạnh \(AB\). Tính số đo của góc nhị diện \(\left[ {M,SO,D} \right]\).
Phương pháp giải - Xem chi tiết
‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
‒ Cách tính chứng minh đường thẳng vuông góc với mặt phẳng: Chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải chi tiết
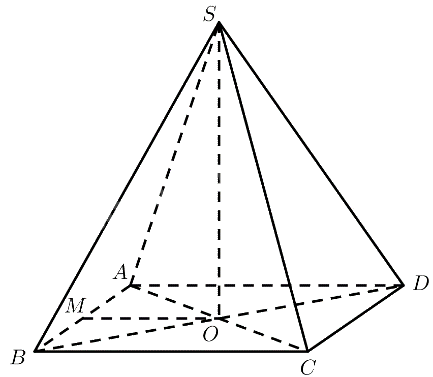
a) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)
Tam giác \(SAC\) là tam giác đều \( \Rightarrow \widehat {SAO} = {60^ \circ }\)
\( \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = {60^ \circ }\)
b) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\)
\( \Rightarrow \left( {SA,\left( {SB{\rm{D}}} \right)} \right) = \left( {SA,SO} \right) = \widehat {ASO} = \frac{1}{2}\widehat {ASC} = {30^ \circ }\)
c) \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot MO,SO \bot DO\)
Vậy \(\widehat {MO{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,SO,D} \right]\)
\(ABCD\) là hình vuông \(\widehat {AOD} = {90^ \circ }\)
\(\Delta AMO\) vuông cân tại \(M \Rightarrow \widehat {AOM} = {45^ \circ }\)
\( \Rightarrow \widehat {MO{\rm{D}}} = \widehat {AOM} + \widehat {AO{\rm{D}}} = {45^ \circ } + {90^ \circ } = {135^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {M,SO,D} \right]\) bằng \({135^ \circ }\).
Bài 2 trang 94 SGK Toán 11 tập 2 - Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài toán này yêu cầu học sinh phải nắm vững các khái niệm về đạo hàm của hàm số, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 2 thường xoay quanh việc xét tính đơn điệu của hàm số. Cụ thể, học sinh cần:
Để giải Bài 2 trang 94 SGK Toán 11 tập 2 - Cánh diều, chúng ta sẽ thực hiện các bước sau:
Sử dụng các quy tắc tính đạo hàm đã học, ta tính đạo hàm của hàm số. Ví dụ, nếu hàm số là f(x) = x2 + 2x + 1, thì f'(x) = 2x + 2.
Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0. Đồng thời, xác định các điểm mà đạo hàm không xác định (ví dụ: mẫu số bằng 0).
Chia trục số thành các khoảng dựa trên các điểm tìm được ở bước 2. Chọn một giá trị đại diện trong mỗi khoảng và tính dấu của f'(x) tại giá trị đó. Lập bảng xét dấu f'(x) để xác định dấu của f'(x) trên mỗi khoảng.
| Khoảng | f'(x) | Kết luận |
|---|---|---|
| (-∞, -1) | Âm | Hàm số nghịch biến |
| (-1, +∞) | Dương | Hàm số đồng biến |
Dựa vào bảng xét dấu f'(x), ta kết luận về khoảng đồng biến và nghịch biến của hàm số. Ví dụ, nếu f'(x) > 0 trên khoảng (a, b), thì hàm số đồng biến trên khoảng (a, b).
Xét hàm số f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
| Khoảng | f'(x) | Kết luận |
|---|---|---|
| (-∞, 0) | Dương | Hàm số đồng biến |
| (0, 2) | Âm | Hàm số nghịch biến |
| (2, +∞) | Dương | Hàm số đồng biến |
Vậy hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2).
Khi giải Bài 2 trang 94 SGK Toán 11 tập 2 - Cánh diều, cần chú ý:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 11 tập 2 - Cánh diều hoặc các đề thi thử Toán 11.
Hy vọng bài giải này sẽ giúp bạn hiểu rõ hơn về Bài 2 trang 94 SGK Toán 11 tập 2 - Cánh diều. Chúc bạn học tập tốt!