Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2 theo chương trình Cánh Diều. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, đặc biệt là với những chủ đề mới.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt nhất trong học tập.
Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí (M)
Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí \(M\) trên tường có độ cao so với nền nhà là \(MH = 80cm\). Quan sát Hình 61, nền nhà gợi nên mặt phẳng \(\left( P \right)\), cho biết độ dài đoạn thẳng \(MH\) gợi nên khái niệm gì trong hình học liên quan đến điểm \(M\) và mặt phẳng \(\left( P \right)\).
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
Độ dài đoạn thẳng \(MH\) gợi nên khái niệm khoảng cách từ một điểm đến một mặt phẳng.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),AI \bot BC\left( {I \in BC} \right)\), \(AH \bot SI\left( {H \in SI} \right)\). Chứng minh rằng khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(AH\).
Phương pháp giải:
Chứng minh \(AH \bot \left( {SBC} \right)\).
Lời giải chi tiết:
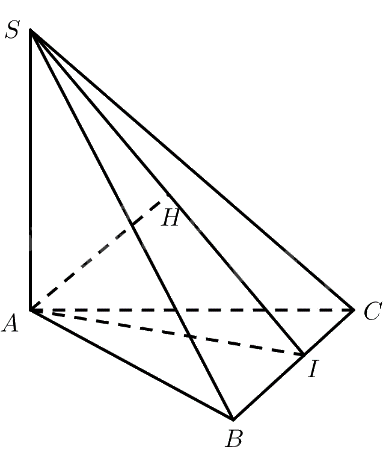
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\\AI \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAI} \right)\\\left. \begin{array}{l} \Rightarrow BC \bot AH\\AH \bot SI\end{array} \right\} \Rightarrow AH \bot \left( {SBC} \right)\end{array}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = AH\).
Mục 2 của SGK Toán 11 tập 2 Cánh Diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để giải quyết thành công các bài tập trong mục này. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 100 và 101, đồng thời phân tích các phương pháp giải hiệu quả.
Trước khi đi vào giải bài tập, chúng ta cần xác định rõ nội dung chính của Mục 2. Thông thường, mục này sẽ đề cập đến các khái niệm, định lý và tính chất quan trọng liên quan đến một chủ đề cụ thể. Việc hiểu rõ các khái niệm này sẽ giúp bạn tiếp cận bài tập một cách dễ dàng hơn.
Bài tập 1 thường yêu cầu giải các phương trình lượng giác cơ bản, ví dụ như sin(x) = a, cos(x) = a, tan(x) = a, cot(x) = a. Để giải các phương trình này, bạn cần nắm vững các công thức lượng giác cơ bản và các phương pháp giải phương trình lượng giác đã học.
Ví dụ: Giải phương trình sin(x) = 1/2
Lời giải: Phương trình sin(x) = 1/2 có các nghiệm là x = π/6 + k2π và x = 5π/6 + k2π, với k là số nguyên.
Bài tập 2 thường yêu cầu giải các phương trình lượng giác phức tạp hơn, ví dụ như phương trình chứa các hàm lượng giác khác nhau, phương trình lượng giác vô tỷ. Để giải các phương trình này, bạn cần sử dụng các kỹ năng biến đổi lượng giác và các phương pháp giải phương trình nâng cao.
Ví dụ: Giải phương trình 2sin2(x) - 3sin(x) + 1 = 0
Lời giải: Đặt t = sin(x), phương trình trở thành 2t2 - 3t + 1 = 0. Giải phương trình bậc hai này, ta được t = 1/2 hoặc t = 1. Từ đó, ta tìm được các nghiệm của phương trình lượng giác ban đầu.
Bài tập 3 thường yêu cầu ứng dụng phương trình lượng giác vào giải quyết các bài toán thực tế, ví dụ như bài toán về dao động điều hòa, bài toán về góc và khoảng cách. Để giải các bài toán này, bạn cần phân tích bài toán, xây dựng mô hình toán học và sử dụng các công thức lượng giác phù hợp.
Việc giải bài tập mục 2 trang 100, 101 SGK Toán 11 tập 2 - Cánh Diều đòi hỏi sự nắm vững kiến thức lý thuyết, kỹ năng giải bài tập và sự kiên trì. Hy vọng rằng với những lời giải chi tiết và phương pháp giải hiệu quả được trình bày trong bài viết này, bạn sẽ tự tin hơn trong việc học tập và đạt kết quả tốt nhất.
| Hàm lượng giác | Công thức |
|---|---|
| sin(x) | Đối diện / Cạnh huyền |
| cos(x) | Kề / Cạnh huyền |
| tan(x) | Đối diện / Kề |