Bài 4 trang 88 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Cánh Diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải quyết bài toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho tứ diện ABCD có (AB bot (BCD),BC bot CD). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng:
Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành. Tam giác ABC nhọn có trực tâm H là hình chiếu của S trên (ABCD). Chứng minh rằng:
a) SA \(\bot\) AD;
b) SC \(\bot\) CD.
Phương pháp giải - Xem chi tiết
Dựa vào quan hệ từ vuông góc đến song song trong không gian để chứng minh
Lời giải chi tiết
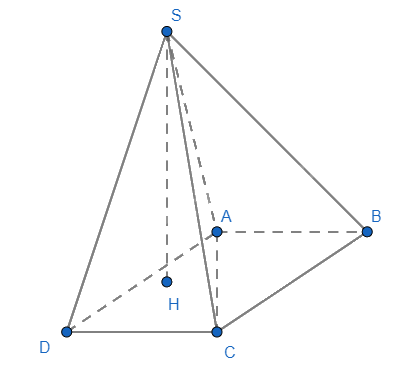
a) Vì SH \(\bot\) (ABCD) nên AH là hình chiếu của SA trên mặt phẳng (ABCD). Mà AH \(\bot\) BC, AD // BC => AH \(\bot\) AD. Theo định lí ba đường vuông góc ta có SA \(\bot\) AD.
b) Vì SH \(\bot\) (ABCD) nên HC là hình chiếu của SC trên mặt phẳng (ABCD). Mà AB \(\bot\) HC, AB // CD => HC \(\bot\) CD. Theo định lí 3 đường vuông góc ta có SC \(\bot\) CD.
Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh Diều yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tốc độ thay đổi của đại lượng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức đạo hàm cơ bản, cũng như kỹ năng phân tích và giải quyết bài toán.
Bài toán thường yêu cầu tính đạo hàm của một hàm số tại một điểm cụ thể, hoặc tìm đạo hàm của hàm số theo một biến số nào đó. Ngoài ra, bài toán có thể yêu cầu học sinh sử dụng đạo hàm để giải quyết các bài toán thực tế, chẳng hạn như tính vận tốc, gia tốc, hoặc tốc độ thay đổi của một đại lượng nào đó.
Để giải quyết bài toán này, học sinh có thể áp dụng các phương pháp sau:
Giả sử chúng ta có hàm số f(x) = x2 + 2x + 1. Để tính đạo hàm của hàm số này tại điểm x = 1, chúng ta có thể áp dụng các công thức đạo hàm cơ bản và quy tắc đạo hàm như sau:
f'(x) = 2x + 2
f'(1) = 2(1) + 2 = 4
Vậy, đạo hàm của hàm số f(x) tại điểm x = 1 là 4.
Khi giải quyết bài toán về đạo hàm, học sinh cần lưu ý các điểm sau:
Để củng cố kiến thức về đạo hàm, học sinh có thể giải các bài tập tương tự sau:
Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh Diều là một bài toán quan trọng giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải quyết bài toán. Bằng cách nắm vững các khái niệm và công thức đạo hàm cơ bản, áp dụng các quy tắc đạo hàm một cách chính xác, và phân tích bài toán một cách cẩn thận, học sinh có thể giải quyết bài toán này một cách hiệu quả.
Hy vọng rằng, với lời giải chi tiết và dễ hiểu tại giaitoan.edu.vn, học sinh sẽ tự tin hơn trong việc học tập và ôn luyện môn Toán 11.