Bài 4 trang 94 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các công thức đạo hàm cơ bản và kỹ năng giải quyết bài toán liên quan đến đạo hàm của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4 trang 94 SGK Toán 11 tập 2 - Cánh diều, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
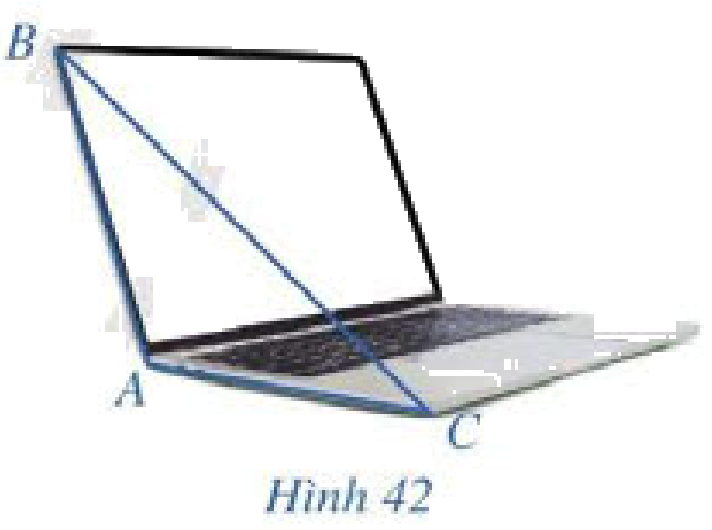
Trong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện
Đề bài
Trong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện. Ta gọi số đo góc nhị diện đó là độ mở của màn hình máy tính. Tính độ mở của màn hình máy tính theo đơn vị độ, biết tam giác \(ABC\) có độ dài các cạnh là \(AB = AC = 30{\rm{ }}cm\) và \(BC = 30\sqrt 3 {\rm{ }}cm\).
Phương pháp giải - Xem chi tiết
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải chi tiết
Gọi \(d\) là đường thẳng chứa bản lề của máy tính.
\(d \bot AB,d \bot AC\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện cần tính.
Xét \(\Delta ABC\) có:
\(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2{\rm{A}}B.AC}} = \frac{{{{30}^2} + {{30}^2} - {{\left( {30\sqrt 3 } \right)}^2}}}{{2.30.30}} = - \frac{1}{2} \Rightarrow \widehat {BAC} = {120^ \circ }\)
Vậy độ mở của màn hình máy tính bằng \({120^ \circ }\).
Bài 4 trang 94 SGK Toán 11 tập 2 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 4 yêu cầu học sinh giải các bài toán liên quan đến việc tìm đạo hàm của hàm số, xác định khoảng đơn điệu của hàm số và tìm cực trị của hàm số. Cụ thể, bài tập có thể yêu cầu:
Để giải Bài 4 trang 94 SGK Toán 11 tập 2 - Cánh diều, học sinh cần nắm vững các kiến thức sau:
Dưới đây là ví dụ về lời giải chi tiết cho một bài tập trong Bài 4:
Ví dụ: Tìm đạo hàm của hàm số f(x) = x^3 - 3x^2 + 2x.
Lời giải:
f'(x) = 3x^2 - 6x + 2
Để tìm khoảng đồng biến, nghịch biến của hàm số, ta xét dấu của f'(x):
f'(x) = 0 khi 3x^2 - 6x + 2 = 0. Giải phương trình này, ta được x1 = (3 - √3)/3 và x2 = (3 + √3)/3.
Ta có bảng xét dấu:
| x | -∞ | (3 - √3)/3 | (3 + √3)/3 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | + |
Vậy hàm số đồng biến trên các khoảng (-∞; (3 - √3)/3) và ((3 + √3)/3; +∞), nghịch biến trên khoảng ((3 - √3)/3; (3 + √3)/3).
Khi giải Bài 4 trang 94 SGK Toán 11 tập 2 - Cánh diều, học sinh cần lưu ý những điều sau:
Để rèn luyện kỹ năng giải bài tập về đạo hàm, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 11 tập 2 - Cánh diều và các tài liệu tham khảo khác.
Hy vọng với lời giải chi tiết và hướng dẫn giải Bài 4 trang 94 SGK Toán 11 tập 2 - Cánh diều trên đây, các em học sinh sẽ hiểu rõ hơn về bài tập này và có thể tự tin giải các bài tập tương tự.