Bài 2 trang 116 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Cánh Diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho hình hộp chữ nhật \(MNPQ.M'N'P'Q'\) có \(MN = 2a,MQ = 3a,\) \(MM' = 4a\).
Đề bài
Cho hình hộp chữ nhật \(MNPQ.M'N'P'Q'\) có \(MN = 2a,MQ = 3a,\) \(MM' = 4a\). Khoảng cách giữa hai đường thẳng \(NP\) và \(M'N'\) bằng:
A. \(2a\).
B. \(3a\).
C. \(4a\).
D. \(5a\).
Phương pháp giải - Xem chi tiết
Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
Lời giải chi tiết
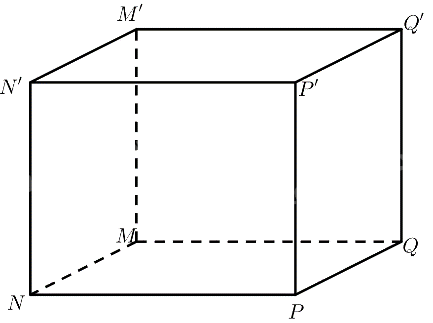
\(\begin{array}{l}NN' \bot \left( {MNPQ} \right) \Rightarrow NN' \bot NP\\NN' \bot \left( {M'N'P'Q'} \right) \Rightarrow NN' \bot M'N'\\ \Rightarrow d\left( {NP,M'N'} \right) = NN' = MM' = 4a\end{array}\)
Chọn C.
Bài 2 trang 116 SGK Toán 11 tập 2 - Cánh Diều yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tốc độ thay đổi của đại lượng. Để giải bài tập này một cách hiệu quả, trước hết cần nắm vững các khái niệm cơ bản về đạo hàm, bao gồm:
Bài tập thường xoay quanh các tình huống thực tế, ví dụ như tính vận tốc của một vật chuyển động, tính tốc độ tăng trưởng của một loài vi khuẩn, hoặc tính tốc độ thay đổi của lợi nhuận trong kinh doanh. Để giải quyết các bài toán này, học sinh cần:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu tính vận tốc của một vật chuyển động theo hàm số s(t) = 2t2 + 3t + 1, trong đó s(t) là quãng đường vật đi được sau thời gian t giây.
Bước 1: Tính đạo hàm của hàm số s(t).
s'(t) = 4t + 3
Bước 2: Giải thích kết quả.
Đạo hàm s'(t) biểu thị vận tốc của vật tại thời điểm t. Ví dụ, tại thời điểm t = 2 giây, vận tốc của vật là s'(2) = 4(2) + 3 = 11 m/s.
Để nắm vững kiến thức về đạo hàm và ứng dụng của nó, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, việc tìm hiểu các ứng dụng thực tế của đạo hàm trong các lĩnh vực khác nhau (ví dụ: vật lý, kinh tế, sinh học) cũng sẽ giúp học sinh hiểu sâu sắc hơn về tầm quan trọng của đạo hàm.
Ngoài SGK Toán 11 tập 2 - Cánh Diều, học sinh có thể tham khảo thêm các tài liệu sau:
Bài 2 trang 116 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Bằng cách nắm vững các khái niệm cơ bản, luyện tập thường xuyên và tìm hiểu các ứng dụng thực tế, học sinh có thể tự tin giải quyết các bài toán liên quan đến đạo hàm.