Chào mừng bạn đến với bài giải Bài 1 trang 94 SGK Toán 11 tập 2 - Cánh diều tại giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, từng bước, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin chinh phục môn Toán.
\(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình thoi cạnh \(a\) và \(AC = a\).
Đề bài
\(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình thoi cạnh \(a\) và \(AC = a\).
a) Tính số đo của góc nhị diện \(\left[ {B,SA,C} \right]\).
b) Tính số đo của góc nhị diện \(\left[ {B,SA,D} \right]\).
c) Biết \(SA = a\), tính số đo của góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\).
Phương pháp giải - Xem chi tiết
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
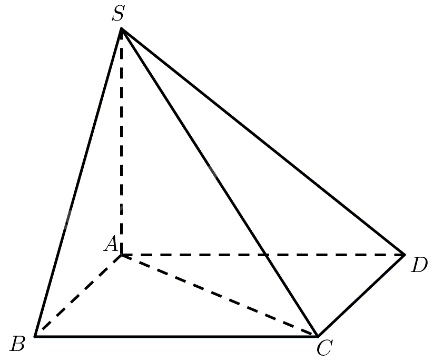
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(AB = BC = AC = a \Rightarrow \Delta ABC\) đều \( \Rightarrow \widehat {BA{\rm{C}}} = \widehat {ABC} = {60^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({60^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình thoi \( \Rightarrow \widehat {BA{\rm{D}}} = {180^ \circ } - \widehat {ABC} = {180^ \circ } - {60^ \circ } = {120^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({120^ \circ }\).
c) \(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{a} = 1 \Rightarrow \widehat {SCA} = {45^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^ \circ }\).
Bài 1 trang 94 SGK Toán 11 tập 2 - Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giải quyết bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần khảo sát là: y = x3 - 3x2 + 2
Bước 1: Tính đạo hàm cấp nhất
y' = 3x2 - 6x
Bước 2: Tìm điểm dừng
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Bước 3: Xét dấu đạo hàm cấp nhất
Trên khoảng (-∞; 0), y' > 0, hàm số đồng biến.
Trên khoảng (0; 2), y' < 0, hàm số nghịch biến.
Trên khoảng (2; +∞), y' > 0, hàm số đồng biến.
Bước 4: Tính đạo hàm cấp hai
y'' = 6x - 6
Bước 5: Xác định điểm uốn
6x - 6 = 0 ⇔ x = 1
Bước 6: Khảo sát hàm số
Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.
Hàm số có điểm uốn tại x = 1.
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Bài 1 trang 94 SGK Toán 11 tập 2 - Cánh diều. Chúc bạn học tập tốt!