Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 77 SGK Toán 11 tập 2 - Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập này thuộc chương trình học Toán 11 tập 2, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm.
Trong mặt phẳng cho hai đường thẳng a, b.
Trong mặt phẳng cho hai đường thẳng a, b.
a) Nếu a và b cắt nhau tại O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?
b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?
c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?
Phương pháp giải:
Dựa vào các kiến thức đã học trong mặt phẳng để trả lời câu hỏi
Lời giải chi tiết:
a) Nếu a và b cắt nhau tại O thì: \(0^\circ \le \left( {a,b} \right) \le 90^\circ \)
b) Nếu a // b thì không có góc tạo bởi a và b
c) Nếu a và b trùng nhau thì góc giữa a và b bằng \(0^\circ \)
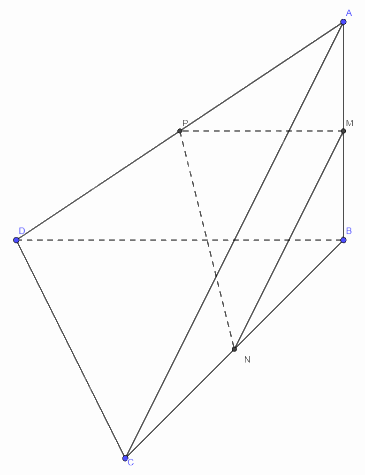
Cho tứ diện ABCD có M, N, P lần lượt là trung điểm của AB, BC, DA. Biết tam giác MNP đều. Tính góc giữa hai đường thẳng AC và BD.

Phương pháp giải:
Dựa vào kiến thức vừa học để làm bài
Lời giải chi tiết:
Xét \(\Delta ACB\)có:
N là trung điểm BC
M là trung điểm AB
=> MN là đường trung bình của tam giác ABC
=> MN // AC
Xét tam giác ABD có:
P là trung điểm AD
M là trung điểm AB
=> MP là đường trung bình của tam giác ABD
=> MP // BD
Ta có \(\left( {AC;BD} \right) = \left( {MN;MP} \right) = \widehat {NMP} = 60^\circ \)
Mục 1 trang 77 SGK Toán 11 tập 2 - Cánh Diều là một phần quan trọng trong chương trình học về đạo hàm. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về định nghĩa đạo hàm, các quy tắc tính đạo hàm và ứng dụng của đạo hàm để giải quyết các bài toán thực tế.
Để tính đạo hàm của hàm số này, ta sử dụng quy tắc tính đạo hàm của tổng, hiệu và lũy thừa:
y' = 3x2 + 4x - 5
Ta sử dụng quy tắc tích để tính đạo hàm:
y' = 2x(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Đầu tiên, ta tính đạo hàm cấp một y':
y' = 4x3 - 8x
Sau đó, ta tính đạo hàm cấp hai y'' bằng cách lấy đạo hàm của y':
y'' = 12x2 - 8
Để tìm cực trị, ta thực hiện các bước sau:
Để khảo sát hàm số, ta thực hiện các bước sau:
| x | -∞ | -1 | 1 | +∞ | |
|---|---|---|---|---|---|
| y' | + | 0 | - | 0 | + |
| y | ↗ | 3 | ↘ | -1 | ↗ |
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập trong Mục 1 trang 77 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt!