Chào mừng các em học sinh đến với lời giải chi tiết Bài 1 trang 109 SGK Toán 11 tập 1 - Cánh Diều. Bài học này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến phép biến hóa lượng giác.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
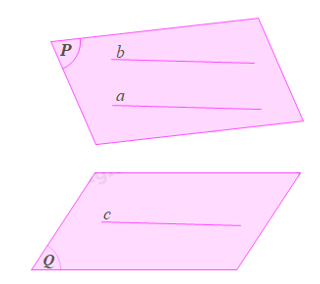
Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?
Đề bài
Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?
Phương pháp giải - Xem chi tiết
Theo dấu hiệu nhận biết hai mặt phẳng song song:
Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải chi tiết
Trường hợp a cắt b theo dấu hiệu nhận biết hai mặt phẳng song song thì ý kiến đúng
Trường hợp a không cắt b thì a // b
Ta có: a thuộc (P), a // (Q)
B thuộc (P), b // (Q)
Do đó: (P) // (Q)
Vậy ý kiến đúng
Bài 1 trang 109 SGK Toán 11 tập 1 - Cánh Diều yêu cầu chúng ta giải các phương trình lượng giác cơ bản. Để giải quyết bài toán này, chúng ta cần nắm vững các công thức lượng giác và các phương pháp giải phương trình lượng giác đã học.
Bài tập này bao gồm các phương trình lượng giác với các hàm sin, cosin, tang và cotang. Các phương trình có thể ở dạng đơn giản hoặc phức tạp hơn, đòi hỏi chúng ta phải sử dụng các kỹ năng biến đổi lượng giác để đưa về dạng cơ bản và giải.
Để giải các phương trình lượng giác, chúng ta có thể sử dụng các phương pháp sau:
Câu a: Giải phương trình sinx = 1/2
Phương trình sinx = 1/2 có nghiệm là:
Với k là số nguyên.
Câu b: Giải phương trình cosx = -√3/2
Phương trình cosx = -√3/2 có nghiệm là:
Với k là số nguyên.
Câu c: Giải phương trình tanx = 1
Phương trình tanx = 1 có nghiệm là:
Với k là số nguyên.
Câu d: Giải phương trình cotx = 0
Phương trình cotx = 0 có nghiệm là:
Với k là số nguyên.
Khi giải phương trình lượng giác, cần chú ý đến điều kiện xác định của phương trình. Ví dụ, với phương trình tanx = a, x không được bằng (π/2) + kπ. Với phương trình cotx = a, x không được bằng kπ.
Để rèn luyện kỹ năng giải phương trình lượng giác, các em có thể làm thêm các bài tập tương tự trong SGK Toán 11 tập 1 - Cánh Diều và các tài liệu tham khảo khác.
Bài 1 trang 109 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp các em củng cố kiến thức về phương trình lượng giác. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!