Giải mục 1 trang 105, 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều

Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 Cánh Diều, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.

Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 1 trang 105, 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều. Các lời giải được trình bày một cách rõ ràng, logic, kèm theo các ví dụ minh họa cụ thể.

Trong không gian cho hai mặt phẳng phân biệt (P) và (Q). Nếu (P) và (Q) có một điểm chung thì chúng có bao nhiêu điểm chung? Các điểm chung đó có tính chất gì?

Hoạt động 1

Trong không gian cho hai mặt phẳng phân biệt (P) và (Q).

Nếu (P) và (Q) có một điểm chung thì chúng có bao nhiêu điểm chung? Các điểm chung đó có tính chất gì?

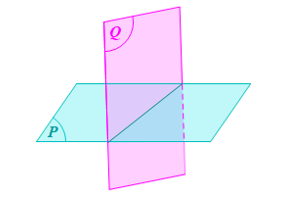
Giải mục 1 trang 105, 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều 1

Phương pháp giải:

Quan sát hình vẽ

Lời giải chi tiết:

Đối với hai mặt phẳng phân biệt (P) và (Q) trong không gian, có hai khả năng xảy ra:

- Hai mặt phẳng (P) và (Q) có 1 điểm chung. Khi đó, chúng có vô số điểm chung và các điểm chung đó cùng nằm trên một đường thẳng.

Luyện tập 1

Nêu ví dụ trong thực tiễn minh họa hình ảnh hai mặt phẳng song song.

Phương pháp giải:

Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung

Lời giải chi tiết:

Trong thực tiễn có nhiều hình ảnh về hai mặt phẳng song song: các mặt của giá để đồ, trần nhà và sàn nhà, hai bức tường đối diện nhau,…

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải mục 1 trang 105, 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều – hành trang không thể thiếu trong chuyên mục toán 11 trên nền tảng soạn toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải mục 1 trang 105, 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều: Tổng quan và Phương pháp giải

Mục 1 của SGK Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức cơ bản về giới hạn của hàm số. Đây là một khái niệm quan trọng, nền tảng cho việc học tập các chương trình Toán học nâng cao hơn. Việc nắm vững các định nghĩa, tính chất và phương pháp tính giới hạn là vô cùng cần thiết.

Các kiến thức trọng tâm trong Mục 1

Định nghĩa giới hạn của hàm số tại một điểm: Hiểu rõ khái niệm hàm số có giới hạn tại một điểm, điều kiện để hàm số có giới hạn.
Tính chất của giới hạn: Nắm vững các tính chất cơ bản của giới hạn như giới hạn của tổng, hiệu, tích, thương, lũy thừa.
Các dạng giới hạn cơ bản: Biết cách tính giới hạn của các hàm số đơn giản như hàm đa thức, hàm phân thức.
Phương pháp tính giới hạn: Sử dụng các phương pháp như phương pháp chia, phương pháp nhân liên hợp, phương pháp sử dụng định lý giới hạn.

Giải chi tiết các bài tập trang 105, 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều

Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1, trang 105, 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều:

Bài 1: (Trang 105)

Đề bài: Tính các giới hạn sau: a) lim (x→2) (x^2 + 1); b) lim (x→-1) (3x - 2)

Lời giải:

a) lim (x→2) (x^2 + 1) = 2^2 + 1 = 5
b) lim (x→-1) (3x - 2) = 3*(-1) - 2 = -5

Bài 2: (Trang 106)

Đề bài: Tính các giới hạn sau: a) lim (x→3) (x^2 - 9)/(x - 3); b) lim (x→1) (x^3 - 1)/(x - 1)

Lời giải:

a) lim (x→3) (x^2 - 9)/(x - 3) = lim (x→3) (x - 3)(x + 3)/(x - 3) = lim (x→3) (x + 3) = 6
b) lim (x→1) (x^3 - 1)/(x - 1) = lim (x→1) (x - 1)(x^2 + x + 1)/(x - 1) = lim (x→1) (x^2 + x + 1) = 3

Bài 3: (Trang 107)

Đề bài: ... (Tiếp tục giải các bài tập còn lại tương tự)

Bài 4: (Trang 108)

Đề bài: ... (Tiếp tục giải các bài tập còn lại tương tự)

Lưu ý khi giải bài tập về giới hạn

Kiểm tra điều kiện xác định: Luôn kiểm tra xem mẫu số có bằng 0 hay không trước khi thực hiện các phép tính.
Sử dụng các công thức giới hạn: Nắm vững các công thức giới hạn cơ bản để đơn giản hóa bài toán.
Biến đổi đại số: Sử dụng các phép biến đổi đại số như phân tích đa thức thành nhân tử, nhân liên hợp để đưa bài toán về dạng đơn giản hơn.
Áp dụng định nghĩa giới hạn: Trong một số trường hợp, cần áp dụng định nghĩa giới hạn để chứng minh sự tồn tại của giới hạn.

Ứng dụng của kiến thức về giới hạn

Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học và các ngành khoa học khác. Ví dụ:

Tính đạo hàm: Giới hạn là cơ sở để định nghĩa đạo hàm của hàm số.
Tính tích phân: Giới hạn được sử dụng để tính tích phân xác định.
Giải phương trình: Giới hạn có thể được sử dụng để giải các phương trình phức tạp.
Vật lý: Giới hạn được sử dụng để mô tả các hiện tượng vật lý như vận tốc tức thời, gia tốc tức thời.

Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ hiểu rõ hơn về các bài tập trong mục 1 trang 105, 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt!