Bài 6 trang 65 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến vectơ. Bài tập này đòi hỏi học sinh nắm vững kiến thức về phép cộng, trừ vectơ, tích của một số với vectơ và các tính chất liên quan.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Bài 6, giúp học sinh hiểu rõ bản chất của vấn đề và tự tin giải quyết các bài toán tương tự.
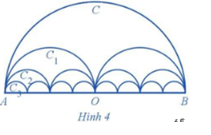
Gọi C là nửa đường tròn đường kính AB = 2R, C1 là đường gồm hai nửa đường tròn đường kính (frac{{AB}}{2},) C2 là đường gồm bốn nửa đường tròn đường kính (frac{{AB}}{4},...) Cn là đường gồm 2n nửa đường tròn đường kính (frac{{AB}}{{{2^n}}},...) (Hình 4). Gọi pn là độ dài của Cn, Sn là diện tích hình phẳng giới hạn bởi Cn và đoạn thẳng AB. a) Tính pn, Sn. b) Tìm giới hạn của các dãy số (pn) và (Sn).
Đề bài
Gọi C là nửa đường tròn đường kính AB = 2R, C1 là đường gồm hai nửa đường tròn đường kính \(\frac{{AB}}{2},\), C2 là đường gồm bốn nửa đường tròn đường kính \(\frac{{AB}}{4},...\)
Gọi pn là độ dài của Cn, Sn là diện tích hình phẳng giới hạn bởi Cn và đoạn thẳng AB.
a) Tính pn, Sn.
b) Tìm giới hạn của các dãy số (pn) và (Sn).
Phương pháp giải - Xem chi tiết
Chu vi hình tròn \(C = \pi d\)
Diện tích hình tròn \(S = \pi {R^2}\)
Lời giải chi tiết
a) Vì Cn là nửa đường tròn đường kính \(\frac{{AB}}{{{2^n}}}\) nên ta có \({p_n} = \frac{1}{2}{.2^n}.\frac{{AB}}{{{2^n}}}.\pi = {2^n}.\frac{R}{{{2^n}}}.\pi = \pi R\)
Đường kính \(\frac{{AB}}{{{2^n}}} = \frac{{2R}}{{{2^n}}}\) nên bánh kính \(\frac{R}{{{2^n}}}\)
\({S_n} = {2^n}.{\left( {\frac{R}{{{2^n}}}} \right)^2}.\frac{\pi }{2} = \frac{{\pi {R^2}}}{2}.\frac{1}{{{2^n}}} = \frac{{\pi {R^2}}}{{{2^{n + 1}}}}\)
b) \(\begin{array}{l}\lim {p_n} = \lim \left( {\pi R} \right) = \pi R\\\lim {S_n} = \lim \frac{{\pi {R^2}}}{{{2^{n + 1}}}} = \lim \left[ {\frac{{\pi {R^2}}}{2}.{{\left( {\frac{1}{2}} \right)}^n}} \right] = \lim \frac{{\pi {R^2}}}{2}.\lim {\left( {\frac{1}{2}} \right)^n} = 0\end{array}\)
Bài 6 trang 65 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về vectơ và ứng dụng vào giải quyết các bài toán hình học. Dưới đây là giải chi tiết từng phần của bài tập này:
Cho hai vectơ a và b khác vectơ 0. Khi nào hai vectơ a và b cùng phương?
Giải:
Hai vectơ a và b được gọi là cùng phương nếu có một số thực k khác 0 sao cho a = kb. Nói cách khác, a và b cùng phương khi và chỉ khi chúng cùng nằm trên một đường thẳng hoặc trùng nhau.
Cho hai vectơ a và b. Khi nào hai vectơ a và b cùng chiều?
Giải:
Hai vectơ a và b được gọi là cùng chiều nếu chúng cùng phương và có cùng hướng. Điều này có nghĩa là, nếu a = kb thì k > 0.
Cho hai vectơ a và b. Khi nào hai vectơ a và b ngược chiều?
Giải:
Hai vectơ a và b được gọi là ngược chiều nếu chúng cùng phương và có hướng ngược nhau. Điều này có nghĩa là, nếu a = kb thì k < 0.
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh AB. Phân tích vectơ CM thành tổng của hai vectơ.
Giải:
Ta có: CM = CA + AM. Vì M là trung điểm của AB, nên AM = 1/2AB. Do đó, CM = CA + 1/2AB.
Cho tam giác ABC. Gọi G là trọng tâm của tam giác. Chứng minh rằng: GA + GB + GC = 0.
Giải:
Vì G là trọng tâm của tam giác ABC, ta có: GA = 2/3AD, GB = 2/3BE, GC = 2/3CF, với D, E, F lần lượt là trung điểm của BC, CA, AB.
Ta có: AD + BE + CF = 0 (theo quy tắc cộng vectơ). Do đó, GA + GB + GC = 2/3(AD + BE + CF) = 0.
Kết luận:
Bài 6 trang 65 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các khái niệm vectơ, phép toán vectơ và ứng dụng của chúng trong hình học. Việc nắm vững kiến thức này sẽ là nền tảng vững chắc cho việc học tập các chương trình Toán học nâng cao hơn.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.