Bài 3 trang 40 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 tập 1, Cánh diều. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
Đề bài
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
a) \(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\)
b) \(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\)
Phương pháp giải - Xem chi tiết
Dựa vào cách vẽ đồ thị đã học để xác định.
Lời giải chi tiết
a) Vẽ đồ thị:
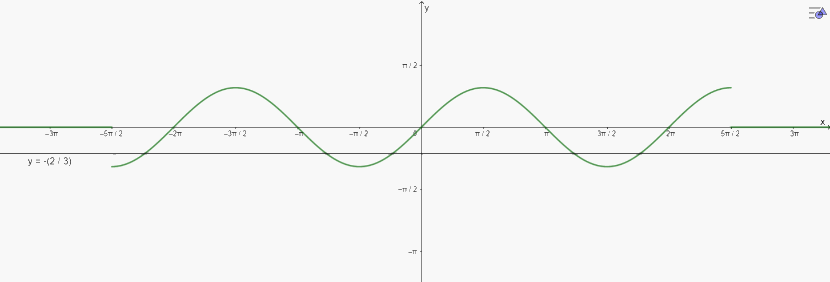
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
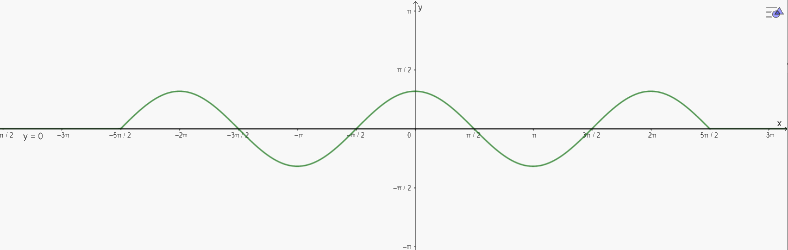
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
Bài 3 trang 40 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng tính giới hạn của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.
Bài 3 yêu cầu tính các giới hạn sau:
lim (x→2) (x^2 - 3x + 2) / (x - 2)
lim (x→-1) (x^3 + 1) / (x + 1)
lim (x→0) (√(x+1) - 1) / x
Để giải quyết bài tập này, chúng ta sẽ sử dụng các phương pháp sau:
Phân tích thành nhân tử: Đối với các biểu thức chứa đa thức, chúng ta có thể phân tích thành nhân tử để rút gọn biểu thức và loại bỏ các yếu tố gây khó khăn trong việc tính giới hạn.
Nhân liên hợp: Đối với các biểu thức chứa căn thức, chúng ta có thể nhân cả tử và mẫu với liên hợp của biểu thức để loại bỏ căn thức và đơn giản hóa biểu thức.
Sử dụng các định lý về giới hạn: Áp dụng các định lý về giới hạn của tổng, hiệu, tích, thương và lũy thừa để tính giới hạn của các biểu thức phức tạp.
a) lim (x→2) (x^2 - 3x + 2) / (x - 2)
Ta phân tích tử thức thành nhân tử:
x^2 - 3x + 2 = (x - 1)(x - 2)
Vậy, biểu thức trở thành:
lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1)
Thay x = 2 vào biểu thức, ta được:
lim (x→2) (x - 1) = 2 - 1 = 1
b) lim (x→-1) (x^3 + 1) / (x + 1)
Ta phân tích tử thức thành nhân tử:
x^3 + 1 = (x + 1)(x^2 - x + 1)
Vậy, biểu thức trở thành:
lim (x→-1) (x + 1)(x^2 - x + 1) / (x + 1) = lim (x→-1) (x^2 - x + 1)
Thay x = -1 vào biểu thức, ta được:
lim (x→-1) (x^2 - x + 1) = (-1)^2 - (-1) + 1 = 1 + 1 + 1 = 3
c) lim (x→0) (√(x+1) - 1) / x
Ta nhân cả tử và mẫu với liên hợp của tử thức:
lim (x→0) (√(x+1) - 1) / x * (√(x+1) + 1) / (√(x+1) + 1) = lim (x→0) (x + 1 - 1) / (x(√(x+1) + 1))
Vậy, biểu thức trở thành:
lim (x→0) x / (x(√(x+1) + 1)) = lim (x→0) 1 / (√(x+1) + 1)
Thay x = 0 vào biểu thức, ta được:
lim (x→0) 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Vậy, kết quả của bài tập là:
lim (x→2) (x^2 - 3x + 2) / (x - 2) = 1
lim (x→-1) (x^3 + 1) / (x + 1) = 3
lim (x→0) (√(x+1) - 1) / x = 1/2
Bài 3 trang 40 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Việc nắm vững các phương pháp giải và luyện tập thường xuyên sẽ giúp học sinh tự tin giải quyết các bài tập tương tự trong các kỳ thi.