Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 5 trang 12 sách giáo khoa Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Quan sát bảng tần số ghép nhóm bao gồm cả tần số tích lũy ở Ví dụ 6
Quan sát bảng tần số ghép nhóm bao gồm cả tần số tích lũy ở Ví dụ 6 và cho biết:
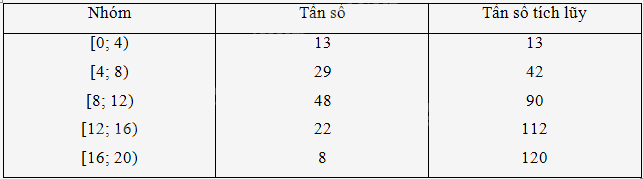
a) Nhóm nào có tần số lớn nhất
b) Đầu mút trái và độ dài của nhóm có tần số lớn nhất bằng bao nhiêu?
Phương pháp giải:
Dựa vào cách đọc bảng tần số và trả lời các câu hỏi trên
Lời giải chi tiết:
a) Nhóm có tần số lớn nhất là: [50 ; 60)
b) Đầu mút trái của nhóm là: 50
Độ dài của nhóm là: 10
Tìm mốt của mẫu số liệu trong Ví dụ 6 (làm tròn các kết quả đến hàng phần mười)

Phương pháp giải:
Dựa vào kiến thức đã học để làm
Lời giải chi tiết:
- Nhóm 3 là nhóm có tần số lớn nhất
- \(u = 8;g = 4;{n_3} = 48\)
- Nhóm 2 có tần số \({n_2} = 29\)
- Nhóm 4 có tần số \({n_4} = 22\)
\( \Rightarrow {M_o} = 8 + \left( {\frac{{48 - 29}}{{4.48 - 29 - 22}}} \right).4 \approx 8,54\)
Mục 5 trang 12 SGK Toán 11 tập 2 - Cánh Diều tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về tập xác định, tập giá trị, tính đơn điệu, cực trị và các ứng dụng của hàm số lượng giác để giải quyết các bài toán cụ thể.
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 5 trang 12, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh xác định tập xác định của một hàm số lượng giác. Để giải bài tập này, học sinh cần nắm vững điều kiện xác định của các hàm số lượng giác cơ bản như sin, cos, tan, cot. Ví dụ, hàm số y = tan(x) chỉ xác định khi cos(x) ≠ 0.
Bài tập này yêu cầu học sinh tìm tập giá trị của một hàm số lượng giác. Để giải bài tập này, học sinh cần nắm vững khoảng giá trị của các hàm số lượng giác cơ bản. Ví dụ, -1 ≤ sin(x) ≤ 1 và -1 ≤ cos(x) ≤ 1.
Bài tập này yêu cầu học sinh xét tính đơn điệu của một hàm số lượng giác trên một khoảng cho trước. Để giải bài tập này, học sinh cần sử dụng đạo hàm của hàm số lượng giác và xét dấu của đạo hàm trên khoảng đó. Nếu đạo hàm dương trên một khoảng thì hàm số đồng biến trên khoảng đó, và nếu đạo hàm âm trên một khoảng thì hàm số nghịch biến trên khoảng đó.
Bài tập này yêu cầu học sinh tìm cực trị của một hàm số lượng giác. Để giải bài tập này, học sinh cần tìm các điểm mà đạo hàm của hàm số bằng 0 hoặc không tồn tại, sau đó xét dấu của đạo hàm để xác định xem các điểm đó là điểm cực đại hay cực tiểu.
Để giải các bài tập về hàm số lượng giác một cách hiệu quả, học sinh cần:
Ví dụ: Giải phương trình sin(2x) = 1.
Lời giải:
Để củng cố kiến thức và kỹ năng giải toán, các em học sinh có thể tự giải thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham gia các diễn đàn toán học trực tuyến để trao đổi kinh nghiệm và học hỏi từ những người khác.
Hy vọng rằng, với những hướng dẫn chi tiết và phương pháp giải toán hiệu quả mà chúng tôi đã trình bày, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 5 trang 12 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt!