Chào mừng bạn đến với bài giải chi tiết Bài 6 trang 94 SGK Toán 11 tập 1 - Cánh Diều tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, lời giải dễ hiểu và các phương pháp tiếp cận khác nhau để giúp bạn nắm vững kiến thức.
Bài 6 tập trung vào các kiến thức về phép biến hình, đặc biệt là phép tịnh tiến và phép quay. Việc hiểu rõ các khái niệm này là nền tảng quan trọng cho các bài học tiếp theo trong chương trình Toán 11.
Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA. a) Xác định giao điểm của CD với hai mặt phẳng (SAB) và (SCD) b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD) c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC)
Đề bài
Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.
a) Xác định giao điểm của CD với hai mặt phẳng (SAB) và (SCD)
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC)
Phương pháp giải - Xem chi tiết
a) Muốn tìm giao điểm của một đường thẳng a và mặt phẳng (P), ta tìm giao điểm của a và một đường thẳng b nằm trong (P):
\(\left\{ \begin{array}{l}a \cap b = M\\b \subset (P)\end{array} \right. \Rightarrow M = a \cap (P)\)
Bước 1: Xác định mp (Q) chứa a
Bước 2: Tìm giao tuyến \(b = (P) \cap (Q)\)
Bước 3: Trong \((Q):a \cap b = M\) mà \(b \subset (P)\)suy ra \(M = a \cap (P)\)
b) Để xác định giao tuyến của hai mặt phẳng, ta tìm điểm chung của chúng. Đường thẳng đi qua hai điểm chung là giao tuyến
Lời giải chi tiết
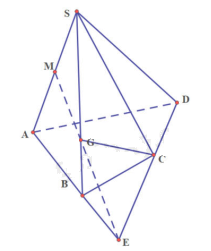
a) Gọi E là giao điểm của AB và CD
Vì AB thuộc mp (SAB) nên E là giao điểm của CD và (SAB)
b) Ta có: S thuộc hai mặt phẳng (SAB) và (SCD)
E thuộc hai mặt phẳng (SAB) và (SCD)
Suy ra SE là giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Trong mp (SAB), gọi G là giao điểm của ME và SB
Mà SB thuộc (SBC),ME thuộc (MCD)
Do đó: G thuộc hai mặt phẳng (MCD) và (SBC)
C thuộc hai mặt phẳng (MCD) và (SBC)
Suy ra CG là giao tuyến của hai mặt phẳng (MCD) và (SBC).
Bài 6 trong SGK Toán 11 tập 1 - Cánh Diều là một bước quan trọng trong việc làm quen với các phép biến hình cơ bản trong hình học. Bài học này tập trung vào hai phép biến hình quan trọng: phép tịnh tiến và phép quay. Hiểu rõ bản chất và cách áp dụng của hai phép biến hình này là nền tảng để giải quyết các bài toán hình học phức tạp hơn.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các khái niệm và tính chất cơ bản của phép tịnh tiến và phép quay:
Dưới đây là lời giải chi tiết cho từng bài tập trong Bài 6:
(Đề bài cụ thể của bài 1)
Lời giải:
(Giải thích chi tiết từng bước giải bài 1, bao gồm cả việc vẽ hình minh họa nếu cần thiết)
(Đề bài cụ thể của bài 2)
Lời giải:
(Giải thích chi tiết từng bước giải bài 2, bao gồm cả việc vẽ hình minh họa nếu cần thiết)
(Đề bài cụ thể của bài 3)
Lời giải:
(Giải thích chi tiết từng bước giải bài 3, bao gồm cả việc vẽ hình minh họa nếu cần thiết)
Để củng cố kiến thức về phép tịnh tiến và phép quay, bạn có thể thực hiện các bài tập sau:
Khi giải các bài tập về phép biến hình, bạn cần lưu ý những điều sau:
Bài 6 trang 94 SGK Toán 11 tập 1 - Cánh Diều là một bài học quan trọng giúp bạn làm quen với các phép biến hình cơ bản. Việc nắm vững kiến thức và kỹ năng giải bài tập trong bài học này sẽ là nền tảng vững chắc cho các bài học tiếp theo trong chương trình Toán 11. Chúc bạn học tập tốt!
| Phép Biến Hình | Định Nghĩa | Tính Chất |
|---|---|---|
| Phép Tịnh Tiến | Biến mỗi điểm thành một điểm sao cho vectơ nối hai điểm tương ứng có cùng hướng và độ dài. | Bảo toàn khoảng cách giữa hai điểm bất kỳ. |
| Phép Quay | Biến mỗi điểm thành một điểm sao cho khoảng cách từ điểm đó đến một điểm cố định (tâm quay) không đổi và góc giữa hai đoạn thẳng nối điểm ban đầu và điểm sau phép quay với tâm quay là một góc cố định (góc quay). | Bảo toàn khoảng cách giữa hai điểm bất kỳ. |