Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 16 trang 95 sách bài tập toán 11 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài tập này một cách cẩn thận, kèm theo các giải thích rõ ràng để giúp bạn nắm vững kiến thức.
Cho hình chóp S.ABC thoả mãn SA = SB = SC.
Đề bài
Cho hình chóp S.ABC thoả mãn SA = SB = SC. Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC. Chứng minh rằng \(SO \bot \left( {ABC} \right).\)
Phương pháp giải - Xem chi tiết
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Lời giải chi tiết
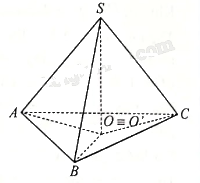
Gọi \(O'\) là hình chiếu của S trên (ABC). Khi đó, \(SO' \bot \left( {ABC} \right).\)
Mà \(O'A,{\rm{ }}O'B,{\rm{ }}O'C\) đều nằm trên (ABC) nên \(SO' \bot O'A,{\rm{ }}SO' \bot O'B,{\rm{ }}SO' \bot O'C.\)
Xét ba tam giác \(SO'A,{\rm{ }}SO'B,{\rm{ }}SO'C\) vuông tại \(O'\) có SA = SB = SC và \(SO'\) chung nên ba tam giác đó bằng nhau. Do đó, \(O'A = O'B = O'C.\)
Suy ra \(O'\) là tâm đường tròn ngoại tiếp của tam giác ABC hay \(O'\) trùng O.
Vậy \(SO \bot \left( {ABC} \right).\)
Bài 16 trang 95 sách bài tập toán 11 - Cánh diều thuộc chương trình học toán 11, tập trung vào các kiến thức về vectơ và các phép toán vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản như:
Dưới đây là lời giải chi tiết cho từng phần của bài 16 trang 95 sách bài tập toán 11 - Cánh diều:
Để tính tổng hai vectơ a và b, ta thực hiện phép cộng từng thành phần tương ứng của hai vectơ. Ví dụ, nếu a = (x1, y1, z1) và b = (x2, y2, z2), thì a + b = (x1 + x2, y1 + y2, z1 + z2). Cần chú ý đến dấu của các thành phần khi thực hiện phép cộng.
Để tính hiệu hai vectơ và tích của một vectơ với một số thực, ta thực hiện các phép toán tương ứng trên từng thành phần của vectơ. Ví dụ, nếu a = (x1, y1, z1) và b = (x2, y2, z2), thì 2a - b = (2x1 - x2, 2y1 - y2, 2z1 - z2). Luôn kiểm tra lại các phép tính để tránh sai sót.
Tích vô hướng của hai vectơ a = (x1, y1, z1) và b = (x2, y2, z2) được tính theo công thức: a.b = x1*x2 + y1*y2 + z1*z2. Tích vô hướng có vai trò quan trọng trong việc xác định góc giữa hai vectơ và kiểm tra tính vuông góc của chúng.
Để tìm hình chiếu của vectơ a lên đường thẳng d, ta cần tìm vectơ chỉ phương của đường thẳng d và sử dụng công thức tính hình chiếu. Việc hiểu rõ về vectơ chỉ phương và công thức tính hình chiếu là rất quan trọng để giải quyết bài toán này.
Lưu ý quan trọng:
Ngoài ra, để hiểu sâu hơn về chương trình học toán 11, bạn có thể tham khảo thêm các tài liệu sau:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn giải bài 16 trang 95 sách bài tập toán 11 - Cánh diều một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tích vô hướng | Một phép toán giữa hai vectơ cho ra một số thực. |