Bài 3 trang 9 sách bài tập Toán 11 - Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập này.
Cho mẫu số liệu ghép nhóm thống kê thời gian sử dụng điện thoại trước khi ngủ
Đề bài
Cho mẫu số liệu ghép nhóm thống kê thời gian sử dụng điện thoại trước khi ngủ (đơn vị: phút) của một người trong 120 ngày như ở Bảng 8. Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu đó (làm tròn các kết quả đến hàng phần mười).
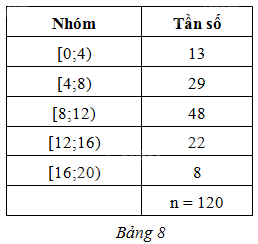
Phương pháp giải - Xem chi tiết
Áp dụng các công thức đã học để xác định các đại lượng tiêu biểu.
Lời giải chi tiết
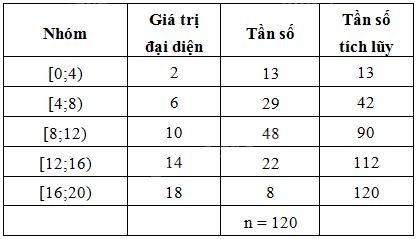
- Thời gian sử dụng điện thoại trung bình trước khi ngủ của một người trong 120 ngày là:
\(\bar x = \frac{{2.13 + 6.29 + 10.48 + 14.22 + 18.8}}{{120}} \approx 9,4\) (phút).
- Ta có: \(\frac{n}{2} = \frac{{120}}{2} = 60\) mà \(42 < 60 < 90.\) Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 60.
Xét nhóm 3 là nhóm [8;12) có \(r = 8,{\rm{ }}d = 4,{\rm{ }}{n_3} = 48\) và nhóm 2 là nhóm [4;8) có \(c{f_2} = 42.\)
Trung vị của mẫu số liệu là:
\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 8 + \left( {\frac{{60 - 42}}{{48}}} \right).4 = 9,5\) (phút).
Tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = {M_e} = 9,5\) (phút).
- Ta có: \(\frac{n}{4} = \frac{{120}}{4} = 30\) mà \(13 < 30 < 42.\) Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 2 là nhóm [4;8) có \(s = 4,{\rm{ }}h = 4,{\rm{ }}{n_2} = 29\) và nhóm 1 là nhóm [0;4) có \(c{f_1} = 13.\)
Tứ phân vị thứ nhất của mẫu số liệu là:
\({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 4 + \left( {\frac{{30 - 13}}{{29}}} \right).4 \approx 6,3\) (phút).
- Ta có: \(\frac{{3n}}{4} = \frac{{3.120}}{4} = 90\) mà \(90 = 90 < 112.\) Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 90.
Xét nhóm 4 là nhóm [12;16) có \(t = 12,{\rm{ }}l = 2,{\rm{ }}{n_4} = 22\) và nhóm 3 là nhóm [8;12) có \(c{f_3} = 90.\)
Tứ phân vị thứ ba của mẫu số liệu là:
\({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 12 + \left( {\frac{{90 - 90}}{{22}}} \right).4 = 12\)(phút).
- Ta thấy: Nhóm 3 ứng với nửa khoảng [8;12) là nhóm có tần số lớn nhất với \(u = 8,{\rm{ }}g = 4,{\rm{ }}{n_3} = 48,{\rm{ }}{n_2} = 29,{\rm{ }}{n_4} = 22.\)
Mốt của mẫu số liệu là:
\({M_0} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 8 + \left( {\frac{{48 - 29}}{{2.48 - 29 - 22}}} \right).4 \approx 9,7\) (phút).
Bài 3 trang 9 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về giới hạn của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.
Bài 3 yêu cầu học sinh tính giới hạn của các hàm số khi x tiến tới một giá trị cụ thể. Các hàm số có thể là các hàm đa thức, hàm phân thức, hoặc các hàm số phức tạp hơn. Việc xác định đúng dạng của hàm số và áp dụng phương pháp tính giới hạn phù hợp là rất quan trọng.
Có nhiều phương pháp để tính giới hạn của hàm số, tùy thuộc vào dạng của hàm số. Một số phương pháp thường được sử dụng bao gồm:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích lời giải chi tiết cho từng câu hỏi trong bài 3.
Lời giải:
Vậy, \lim_{x \to 2} \frac{x^2 - 4}{x - 2} = 4
Lời giải:
Vậy, \lim_{x \to -1} \frac{x^3 + 1}{x + 1} = 3
Khi giải bài tập về giới hạn, học sinh cần lưu ý một số điều sau:
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật, bao gồm:
Hy vọng rằng với hướng dẫn chi tiết này, các bạn học sinh sẽ hiểu rõ hơn về cách giải bài 3 trang 9 sách bài tập Toán 11 - Cánh Diều và có thể áp dụng kiến thức này để giải quyết các bài toán tương tự.