Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 31 trang 81 sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam
Đề bài
Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250 g như trong bảng sau:
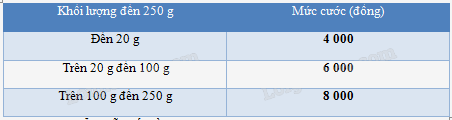
a) Hãy biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp.
b) Hàm số trên có liên tục trên tập xác định hay không?
Phương pháp giải - Xem chi tiết
a) Dựa vào bảng, ta thấy với khối lượng từ 0 đến 20 g thì mức cước là 4000 đồng, từ trên 20 g đến 100 g thì mức cước là 6000 đồng, từ trên 100 g đến 250 g thì mức cước là 8000 đồng. Từ đó ta sẽ có hàm số biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp.
b) Hàm số có tập xác định là \(\left( {0,250} \right]\). Sử dụng các tính chất của hàm số liên tục.
Lời giải chi tiết
a) Dựa vào bảng, ta thấy với khối lượng từ 0 đến 20 g thì mức cước là 4000 đồng, từ trên 20 g đến 100 g thì mức cước là 6000 đồng, từ trên 100 g đến 250 g thì mức cước là 8000 đồng. Như vậy, nếu gọi\(x\) là khối lượng của thư cơ bản và bưu thiếp và \(f\left( x \right)\) là số tiền phải trả thì ta có hàm số: \(f\left( x \right) = \left\{ \begin{array}{l}4000{\rm{ }}\left( {0 < x \le 20} \right)\\6000{\rm{ }}\left( {20 < x \le 100} \right)\\8000{\rm{ }}\left( {100 < x \le 250} \right)\end{array} \right.\).
b) Hàm số có tập xác định là \(\left( {0,250} \right]\).
Ta có \(\mathop {\lim }\limits_{x \to {{20}^ - }} f\left( x \right) = 4000\) và \(\mathop {\lim }\limits_{x \to {{20}^ + }} f\left( x \right) = 6000\). Do \(\mathop {\lim }\limits_{x \to {{20}^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {{20}^ + }} f\left( x \right)\), nên không tồn tại \(\mathop {\lim }\limits_{x \to 20} f\left( x \right)\).
Suy ra hàm số không liên tục tại \(x = 20\).
Mà \(20 \in \left( {0,250} \right]\), ta kết luận hàm số không liên tục trên tập xác định của nó.
Bài 31 trang 81 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Bài tập này thường tập trung vào việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng, tính góc giữa đường thẳng và mặt phẳng, và giải các bài toán ứng dụng liên quan.
Bài 31 thường bao gồm các dạng bài tập sau:
Để giải bài tập về đường thẳng và mặt phẳng, bạn cần nắm vững các kiến thức sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ cung cấp hướng dẫn giải chi tiết cho từng phần của bài 31 trang 81 sách bài tập Toán 11 - Cánh Diều. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích, và kết luận. Ví dụ:)
Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Giải:
Khi giải bài tập về đường thẳng và mặt phẳng, bạn cần chú ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự sau:
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải bài 31 trang 81 sách bài tập Toán 11 - Cánh Diều một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!
| Công thức | Mô tả |
|---|---|
| tan(θ) = d(A, (P)) / AH | Góc giữa đường thẳng và mặt phẳng |
| d(A, (P)) = |MA.n| / ||n|| | Khoảng cách từ điểm A đến mặt phẳng (P) |