Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 40 trang 113 sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn tự tin hơn trong việc chinh phục môn Toán.
Cho hình hộp \(ABCD.A'B'C'D'\).
Đề bài
Cho hình hộp \(ABCD.A'B'C'D'\). Mặt phẳng \(\left( {BA'C'} \right)\) song song với mặt phẳng nào dưới đây?
A. \(\left( {ACD} \right)\)
B. \(\left( {ADD'} \right)\)
C. \(\left( {DCD'} \right)\)
D. \(\left( {AD'C} \right)\)
Phương pháp giải - Xem chi tiết
Chỉ ra hai đường thẳng cắt nhau và song song với \(\left( {BA'C'} \right)\), mặt phẳng chứa hai đường thẳng đó là mặt phẳng cần tìm.
Lời giải chi tiết
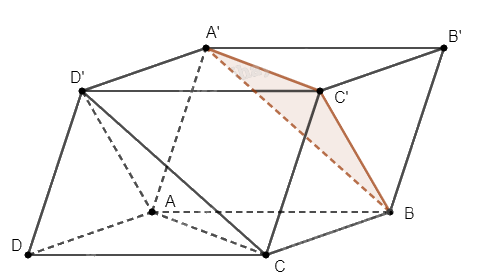
Do hình hộp là hình lăng trụ, các mặt bên là hình bình hành nên ta có \(ADD'A'\) và \(DCC'D'\) là các hình bình hành.
Ta có \(A' \in \left( {ADD'A'} \right) \cap \left( {BA'C'} \right)\) nên hai mặt phẳng \(\left( {ADD'A'} \right)\) và \(\left( {BA'C'} \right)\) có điểm chung, tức là chúng không song song với nhau.
Chứng minh tương tự, hai mặt phẳng \(\left( {BA'C'} \right)\) và \(\left( {DCD'} \right)\) không song song với nhau, và hai mặt phẳng \(\left( {BA'C'} \right)\) và \(\left( {ACD} \right)\) cũng không song song với nhau.
Nhận xét rằng tứ giác \(ACC'A'\) có \(AA' = CC'\) và \(AA'\parallel CC'\) nên nó là hình bình hành. Suy ra \(A'C'\parallel AC\). Do \(AC \subset \left( {AD'C} \right)\) nên \(A'C'\parallel \left( {AD'C} \right)\).
Chứng minh tương tự ta cũng có \(BC'\parallel \left( {AD'C} \right)\). Như vậy \(\left( {BA'C'} \right)\parallel \left( {AD'C} \right)\).
Đáp án đúng D.
Bài 40 trang 113 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về hàm số lượng giác. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác, tính chất của hàm số lượng giác và các phương pháp giải phương trình lượng giác để tìm ra nghiệm.
Bài 40 thường bao gồm các dạng bài tập sau:
Để giải bài 40 trang 113 sách bài tập Toán 11 - Cánh Diều, bạn cần nắm vững các kiến thức sau:
Bài tập: Chứng minh rằng sin2x + cos2x = 1
Lời giải:
Ta có: sin2x + cos2x = (sin x)2 + (cos x)2
Theo định nghĩa sin và cos trong tam giác vuông, ta có: sin x = đối/cạnh huyền và cos x = kề/cạnh huyền
Áp dụng định lý Pitago cho tam giác vuông, ta có: đối2 + kề2 = cạnh huyền2
Suy ra: (sin x)2 + (cos x)2 = (đối/cạnh huyền)2 + (kề/cạnh huyền)2 = (đối2 + kề2)/cạnh huyền2 = cạnh huyền2/cạnh huyền2 = 1
Vậy, sin2x + cos2x = 1 (đpcm)
Để học tốt môn Toán 11, bạn có thể tham khảo các tài liệu sau:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 40 trang 113 sách bài tập Toán 11 - Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!